【简单的小实验】一个数组中的子数组的和的最大值

结对成员：李金吉，赵天

 

要求：

　　实现查找到一个数组的子数组中元素的和的最大值，比如说:

int a[]={9,8,-3,19,-30}

 这时我们发现9+8+-3+19 这个子数组的和是最大的。

想法：

　　如果是人脑的做法，无非从两个开始比较，将两个两个的和计算出来；再三个三个比较，将三个的和计算出来.....

用计算机实现：

　　可以从数组中第一个开始，设置一个辅助数组记录子数组的和；

如图：有个一个数组arr[]; a[0]~a[n]是辅助数组；

a[0]=arr[0];

a[1]=arr[0]+arr[1];

a[2]=arr[0]+arr[1]+arr[2];

a[3]=arr[0]+arr[1]+arr[2]+a[3];

....  

a[7]=arr[1];

a[8]=arr[1]+arr[2];

a[9]=arr[1]+arr[2]+arr[3];

.... 

可以发现a[0]=arr[0];

　　　　a[1]=a[0]+arr[2];

　　　　...　　

　　　　a[n-1]=a[n-2]+arr[n-1];

　　　　...

 

 

通过这种方法可以将这个数组的每个子数组的元素和都遍历出来：

具体代码及单元测试：

#include<iostream>
#define null -858993460
using namespace std;


void main()
{
	int arr[]={8,9,10,-1,20,-30,4};
	int arr2[]={-9,-1,-4,-123};
	int arr3[]={0};
	int arr4[]={7,9,8};
	int arr5[3];

	int test(int list[],int length);

	cout<<test(arr,7)<<endl;
	cout<<test(arr2,4)<<endl;
	cout<<test(arr3,1)<<endl;
	cout<<test(arr4,3)<<endl;
	cout<<test(arr5,0)<<endl;
	


}
int test(int list[],int length)
{
	int a[100]={0},x=0;
	int max;
	int i,j;
	int k=0;

	if(list==NULL||length==0)
	{
		cout<<"error!inter is null!";
		return 0;
	}
	
	
	for(i=0;i<length;i++)
	{
		a[k]=list[i];
		for(j=i;j<length;j++)
		{
			a[k+1]=a[k]+list[j+1];
			k++;
		}
	}
	max=a[0];
	for(i=0;i<k;i++)
	{
		if(max<a[i])
		{
			max=a[i];
		}
		
	}
	return max;
	

}

 

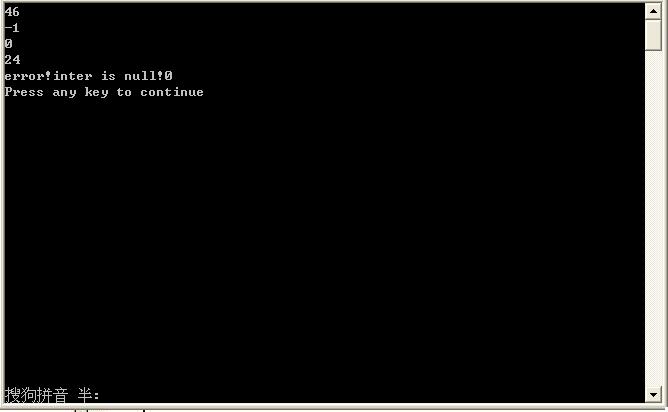
　这种算法的时间复杂度o(n²)

老师说这种算法的时间复杂度可以达到n,通过查阅资料知道，用2分法遍历可是实现时间复杂度O(nlogn)，利用类似数的遍历（递归调用）实现时间复杂度O（n）,

//令cursum(i)表示数组下标以i为起点的最大连续下标最大的和，而maxsum(i)表示前i个元素的最大子数组之和。
//那么我们就可以推出下一个maxsum(i+1)应该为cursum(i+1)和maxsum(i)中选取一个最大值。递推式为：
cursum(i) = max{A[i],cursum(i-1)+A[i]};
maxsum(i) = max{maxsum(i-1),cursum(i+1)};

 

转载于:https://www.cnblogs.com/zhaotian/p/3592560.html