④.AVL树基础

最新推荐文章于 2025-09-07 20:32:33 发布

weixin_30724853

最新推荐文章于 2025-09-07 20:32:33 发布

阅读量67

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/stezqy/p/4293452.html

本文深入讲解AVL树的概念、特点及实现方式，包括单旋转、双旋转操作，并提供了插入和删除节点的具体步骤。

AVL是一种平衡的二叉树。它的作用是避免二叉树形成像链表那样的O(N)结构。

条件：每个节点左子树与右子树的高度最多差1。

我们在进行插入与删除时会改变其平衡性，于是引入旋转：

旋转：

对于需要重新平衡的那个点A来说，分为四种情况：

① 捣乱的在A左儿子的左子树

② 捣乱的在A左儿子的右子树

③ 捣乱的在A右儿子的左子树

④ 捣乱的在A右儿子的右子树

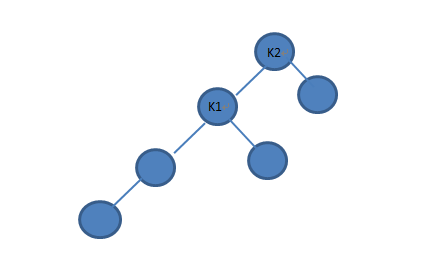比如K2即为A点，捣乱的那个点我们定义为K1的左子节点（反正我们就看需要平衡那个点高度较高的子树：是在左边的左边还是左边的右边balabala）

树的定义：

 1 #include <stdlib.h>
 2 typedef struct AvlNode  *AvlTree;
 3 typedef struct AvlNode  *Position1;
 4 
 5 struct AvlNode{
 6     int Element;
 7     AvlTree left;
 8     AvlTree right;
 9     int Height;
10 };

View Code

单旋转k1成为新的顶点，想象着按着ｋ１左扭右扭

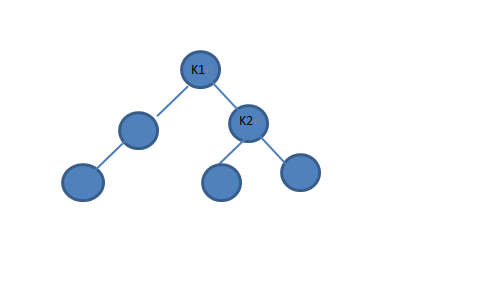
单左旋转用于①：

 1 int Height(Position1 k){
 2     if (k == NULL)
 3         return -1;
 4     else
 5         return k->Height;
 6 }
 7 Position1 SingleRotateLeft(Position1 k2){    //单左旋转
 8     Position1 k1 = k2->left;
 9     k2->left = k1->right;
10     k1->right = k2;
11     k1->Height=(__max(Height(k1->left),k2->Height)+1);
12     k2->Height = (__max(Height(k2->left), Height(k2->right)) + 1);
13     return k1;   //返回现在的顶点
14 
15 }

View Code

单右旋转用于②：

1 Position1 SingleRotateRight(Position1 k2){    //单右旋转
2     Position1 k1 = k2->right;
3     k2->right = k1->left;
4     k1->left = k2;
5     k1->Height = (__max(Height(k1->right), k2->Height) + 1);
6     k2->Height = (__max(Height(k2->left), Height(k2->right)) + 1);
7     return k1;   //返回现在的顶点
8 
9 }

View Code

双旋转：

左-右旋转：（用于②）

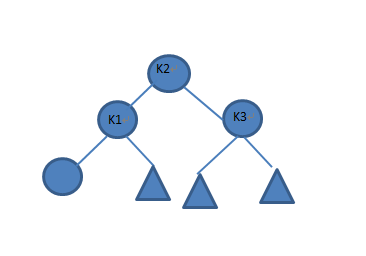
k3是需要重新平衡的那个点，先对k1-k2进行左转，再对k3-k2进行右转

1 Position1 DoubleRotateLeft(AvlTree k3){    //左子树的右子树插入
2     k3->left = SingleRotateRight(k3->left);
3     return SingleRotateLeft(k3);
4 }

View Code

右-左旋转：（用于③）

1 Position1 DoubleRotateRight(AvlTree k3){    //右子树的左子树插入
2     k3->right = SingleRotateLeft(k3->right);
3     return SingleRotateRight(k3);
4 }

View Code

插入：

对于下面那个递归算法：因为插入后只有从插入点到根节点的节点的平衡可能被改变，所以就沿着这条线进行递归更新：

 1 AvlTree  Insert(int x, AvlTree T){
 2     if (T == NULL){
 3         T=(Position1)malloc(sizeof(struct AvlNode));
 4         T->left = T->right = NULL; T->Element = x; T->Height = 0;
 5     }
 6     else{
 7         if (x < T->Element){
 8             T->left=Insert(x, T->left);
 9             if (Height(T->left) - Height(T->right) == 2){
10                 
11                 if (x < T->left->Element)
12                     T=SingleRotateLeft(T);
13                 else
14                     T=DoubleRotateLeft(T);
15 
16             }
17 
18         }
19         else if (x > T->Element){
20             T->right=Insert(x, T->right);
21             if (Height(T->right) - Height(T->left) == 2){
22                 if (x >T->right->Element)
23                     T = SingleRotateRight(T);
24                 else{
25                     
26                     T = DoubleRotateRight(T);
27                 }
28             }
29 
30 
31         }
32     }
33     T->Height = (__max(Height(T->left), Height(T->right)) + 1);//这句应该是对于那些没有旋转的节点更新高度
34     return  T;
35 
36 }

View Code

删除：

 1 Position1 FindMin(AvlTree T){   //对于有两个子节点的删除的辅助函数
 2     if (T->left != NULL)
 3         return FindMin(T->left);
 4     else
 5         return T;
 6 
 7 }
 8 
 9 AvlTree Delete(int x, AvlTree T){
10     int Temp;
11     if (T == NULL){
12         return T;
13     }
14     else{
15         if (x < T->Element){
16             T->left=Delete(x, T->left);
17             if (Height(T->right) - Height(T->left) == 2){    //这里要和插入的注意区别，画图就可以看出哪里不同了
18                 if (T->right->left==NULL) //如果左子节点的右子节点不存在，就用单旋转，否则用双旋转
19                     T = SingleRotateRight(T);
20                 else
21                     T = DoubleRotateRight(T);
22             }
23 
24         }
25 
26         else if (x > T->Element){
27             T->right = Delete(x, T->right);
28             if (Height(T->left) - Height(T->right) == 2){
29                 if (T->left->right==NULL)
30                     T = SingleRotateLeft(T);
31                 else
32                     T = DoubleRotateLeft(T);
33 
34             }
35         }
36         else{
37             if (T->left != NULL&&T->right != NULL){
38                 Temp = T->Element;
39                 T->Element = (FindMin(T->right))->Element;
40                 (FindMin(T->right))->Element = Temp;
41                 T->right = Delete(x, T->right);
42 
43             }
44             else if (T->left == NULL){
45                 T = T->right;
46                 
47             }
48             else
49                 T = T->left;
50         }
51 
52     }
53     if (T != NULL)//T可能是NULL；
54          T->Height = (__max(Height(T->left), Height(T->right)) + 1);
55     return T;
56 }