Java中的Collection和Map(五)--PriorityQueue-优快云博客

本文详细解析Java中的PriorityQueue实现原理，包括构造方法、底层数组调整、扩容机制、add(Ee)方法实现，以及如何通过树形结构直观理解优先队列的调整过程。同时，文章深入探讨了PriorityQueue的特性、使用注意事项及与ArrayList的相似之处。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

　　PriorityQueue java api给出的定义：

　　一个基于优先级堆的无界优先级队列。优先级队列的元素按照其自然顺序进行排序，或者根据构造队列时提供的 Comparator 进行排序，具体取决于所使用的构造方法。优先级队列不允许使用 null 元素。依靠自然顺序的优先级队列还不允许插入不可比较的对象（这样做可能导致 ClassCastException）。

　　此队列的头是按指定排序方式确定的最小元素。如果多个元素都是最小值，则头是其中一个元素——选择方法是任意的。队列获取操作 poll、remove、peek 和 element 访问处于队列头的元素。

　　优先级队列是无界的，但是有一个内部容量，控制着用于存储队列元素的数组大小。它通常至少等于队列的大小。随着不断向优先级队列添加元素，其容量会自动增加。无需指定容量增加策略的细节。

　　此类及其迭代器实现了 Collection 和 Iterator 接口的所有可选方法。方法 iterator() 中提供的迭代器不保证以任何特定的顺序遍历优先级队列中的元素。如果需要按顺序遍历，请考虑使用 Arrays.sort(pq.toArray())。

注意，此实现不是同步的。如果多个线程中的任意线程修改了队列，则这些线程不应同时访问 PriorityQueue 实例。相反，请使用线程安全的 PriorityBlockingQueue 类。

实现注意事项：此实现为排队和出队方法（offer、poll、remove() 和 add）提供 O(log(n)) 时间；为 remove(Object) 和 contains(Object) 方法提供线性时间；为获取方法（peek、element 和 size）提供固定时间。

此类是 Java Collections Framework 的成员。

　　在平时的编程工作中似乎很少碰到PriorityQueue（优先队列），故很多人一开始看到优先队列的时候还会有点迷惑。优先队列本质上就是一个最小堆。堆是什么呢，我们可以这么理解他就是一数组，不过满足于特殊的性质。我们以一种完全二叉树的视角去看这个数组，并用二叉树的上下级关系来映射到数组上面。如果是最大堆，则二叉树的顶点是保存的最大值，最小堆则保存的最小值。

　　PriorityQueue的构造方法：

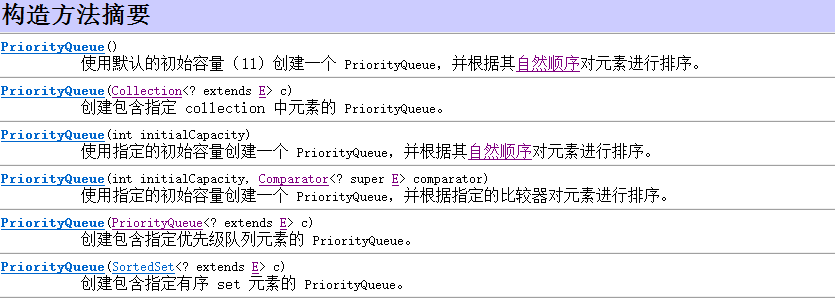
　　java 为我们提供了多重构造方法，当我们想PriorityQueue 传递已结合的时候，PriorityQueue 会存在一个调整堆的过程（通过调用heapify () 方法来实现）：　　

private void heapify() {
        for (int i = (size >>> 1) - 1; i >= 0; i--)
            siftDown(i, (E) queue[i]);
    }

 private void siftDown(int k, E x) {
        if (comparator != null)
            siftDownUsingComparator(k, x);
        else
            siftDownComparable(k, x);
    }

private void siftDownUsingComparator(int k, E x) {
        int half = size >>> 1;
        while (k < half) {
            int child = (k << 1) + 1;
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                comparator.compare((E) c, (E) queue[right]) > 0)
                c = queue[child = right];
            if (comparator.compare(x, (E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = x;
    }

private void siftDownComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;        // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }

　　我们以树的形式来体现底层数组的调整结构：

　　假设我们初始化的时候存在这么一组数据[8,5,7,9,6,1],其对应的树形结构如下：

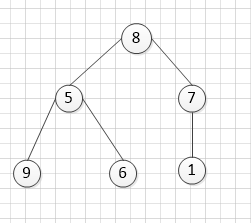
　第一步调整：

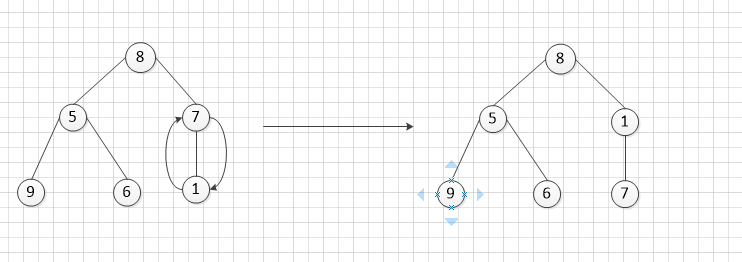
　　第二步调整：

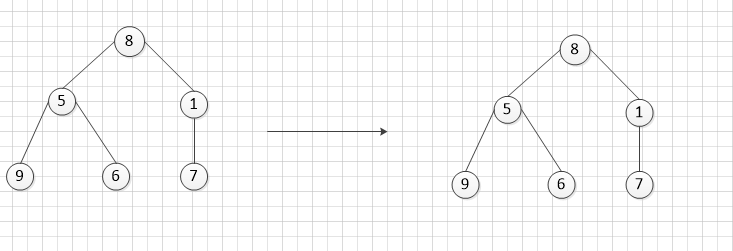
　　第三步调整：

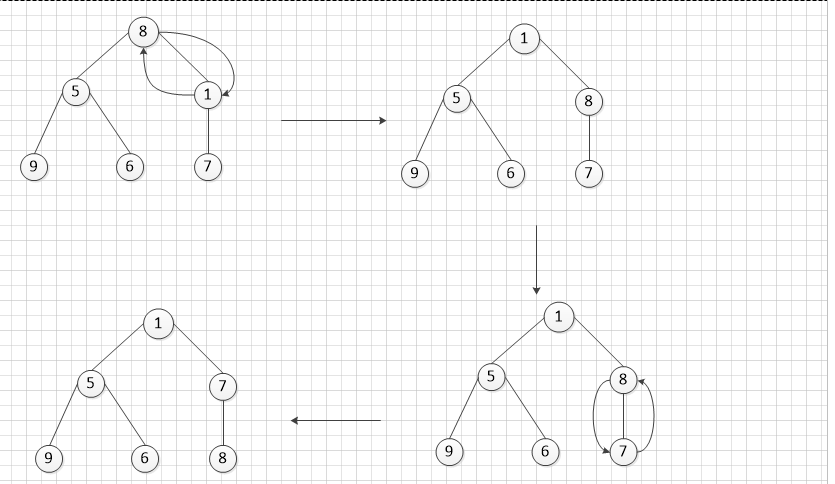
　　按照前面的过程，相信代码就很好理解了。

　　PriorityQueue 底层使用数组来存储数据的，这就跟ArrayList 一样会牵扯到扩容的问题，我们来看下PriorityQueue 是如何扩容的。

private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                         (oldCapacity + 2) :
                                         (oldCapacity >> 1));
        // overflow-conscious code
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }

    private static int hugeCapacity(int minCapacity) {
        if (minCapacity < 0) // overflow
            throw new OutOfMemoryError();
        return (minCapacity > MAX_ARRAY_SIZE) ?
            Integer.MAX_VALUE :
            MAX_ARRAY_SIZE;
    }

　　这部分代码和ArrayList的内部实现代码基本相同，都是先找到合适的数组长度，然后将元素从旧的数组拷贝到新的数组。

　　add (E e) 方法：

public boolean add(E e) {
        return offer(e);
    }

public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e);
        return true;
    }

　　从这段代码我们可以看出 PriorityQueue ，不支持null 而且添加时真正的实现是 siftUp 方法：

private void siftUp(int k, E x) {
        if (comparator != null)
            siftUpUsingComparator(k, x);
        else
            siftUpComparable(k, x);
    }

    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

    private void siftUpUsingComparator(int k, E x) {
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (comparator.compare(x, (E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = x;
    }

　　假如我们初始化的时候PriorityQueue 是空，我们还用[8,5,7,9,6,1]这些数据，调用PriorityQueue 的add(E e) 方法，我们看一下他们的具体过程。这里还采用树形结构来描述。

　　第一次调用add(E e) 方法 e=8,后数据结果为[8];

　　第二次调用add(E e) 方法 e=5,后数据结果为[5,8];

　　第三次调用add(E e) 方法 e=7,后数据结果为[5,8,7];

　第四次调用add(E e) 方法 e=9,后数据结果为[5,8,7,9];

　　第五次调用add(E e) 方法 e=5,后数据结果为[5,6,7,9,8];

　第六次调用add(E e) 方法 e=1,后数据结果为[1,6,5,9,8,7];

　　最后的树结构如下：

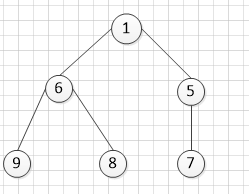
　　注意：们看前面的调整方法不管是siftUp还是siftDown都用了两个方法，一个是用的comparator，还有一个是用的默认比较结果。这样做的目的是考虑到我们要比较的元素不仅仅是数字等类型，也有可能是被定义了可比较的数据类型。对于自定义的数据类型，他们的大小比较定义需要实现comparator接口。

转载于:https://www.cnblogs.com/gaohuiqian/p/5233926.html