Codeforces Round #361 (Div. 2) E. Mike and Geometry Problem 离散化+逆元

E. Mike and Geometry Problem

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's definef([l, r]) = r - l + 1 to be the number of integer points in the segment [l, r] with l ≤ r (say that ). You are given two integers nand k and n closed intervals [li, ri] on OX axis and you have to find:

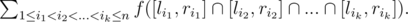
In other words, you should find the sum of the number of integer points in the intersection of any k of the segments.

As the answer may be very large, output it modulo 1000000007 (109 + 7).

Mike can't solve this problem so he needs your help. You will help him, won't you?

Input

The first line contains two integers n and k (1 ≤ k ≤ n ≤ 200 000) — the number of segments and the number of segments in intersection groups respectively.

Then n lines follow, the i-th line contains two integers li, ri ( - 109 ≤ li ≤ ri ≤ 109), describing i-th segment bounds.

Output

Print one integer number — the answer to Mike's problem modulo 1000000007 (109 + 7) in the only line.

Examples

input

3 2
1 2
1 3
2 3

output

5

input

3 3
1 3
1 3
1 3

output

3

input

3 1
1 2
2 3
3 4

output

6

Note

In the first example:

;

;

.

So the answer is 2 + 1 + 2 = 5.

思路：给你n条线段，把线段放进数轴每次处理每个点的贡献，端点另外算；

　　给两组数据

　　2 1

      1 3 

　　3 4

 

      2 1

　　1 3

　　5 6

#include<bits/stdc++.h>
using namespace std;
#define ll __int64
#define esp 0.00000000001
const int N=2e5+10,M=1e6+10,inf=1e9,mod=1e9+7;
struct is
{
    ll l,r;
}a[N];
ll poww(ll a,ll n)//快速幂
{
   ll r=1,p=a;
   while(n)
   {
       if(n&1) r=(r*p)%mod;
       n>>=1;
       p=(p*p)%mod;
   }
   return r;
}
ll flag[N*4];
ll lisan[N*4];
ll sum[N*4];
ll zz[N*2];
int main()
{
    ll x,y,z,i,t;
    scanf("%I64d%I64d",&x,&y);
    int ji=1;
    for(i=0;i<x;i++)
    {
        scanf("%I64d%I64d",&a[i].l,&a[i].r);
        flag[ji++]=a[i].l;
        flag[ji++]=a[i].l+1;
        flag[ji++]=a[i].r;
        flag[ji++]=a[i].r+1;
    }
    sort(flag+1,flag+ji);
    ji=unique(flag+1,flag+ji)-(flag+1);
    int h=1;
    for(i=1;i<=ji;i++)
    lisan[h++]=flag[i];
    memset(flag,0,sizeof(flag));
    for(i=0;i<x;i++)
    {
        int l=lower_bound(lisan+1,lisan+h,a[i].l)-lisan;
        int r=lower_bound(lisan+1,lisan+h,a[i].r)-lisan;
        flag[l]++;
        flag[r+1]--;
    }
    for(i=1;i<=h;i++)
    sum[i]=sum[i-1]+flag[i];
    ll ans=0;
    memset(zz,0,sizeof(zz));
    zz[y]=1;
    for (i=y+1;i<=2*x;i++) zz[i]=((zz[i-1]*i%mod)*poww(i-y,mod-2))%mod;
    for(i=1;i<h;i++)
    {
        int zh=min(sum[i],sum[i-1]);
        ans+=zz[zh]*(lisan[i]-lisan[i-1]-1);
        ans+=zz[sum[i]];
        ans%=mod;
    }
    printf("%I64d\n",ans);
    return 0;
}

 

 

转载于:https://www.cnblogs.com/jhz033/p/5654406.html