Codeforces Round #460 Div. 2 C.D-优快云博客

本文介绍了一个简单的算法问题，即在一个矩阵中计数连续的字符，并使用动态规划与拓扑排序解决了一个涉及字符串和图的问题。

C……没啥好说的……感觉……找一行或一列中有多少个连续的k个‘.’（虽然因为一个i,j写反了搞了好久才改出来orz）

（k==1的时候要特判一下，或者直接ans/2也可以的样子）

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5;
int n,m,k,ans=0;
char mz[2005][2005];
int main()
{
    cin>>n>>m>>k;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        cin>>mz[i][j];
    if(k==1)
    {
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            if(mz[i][j]=='.') ans++;
    }
    else if(k>m&&k>n) ans=0;
    else
    {
    for(int i=0;i<n;i++)
    {
     int cnt=0;
     for(int j=0;j<m;j++)
     {
         if(mz[i][j]=='.')
         {
             cnt++;
             if(cnt>=k)
                ans++;
         }
         else cnt=0;
     }
    }
    for(int i=0;i<m;i++)
    {
     int cnt=0;
     for(int j=0;j<n;j++)
     {
         if(mz[j][i]=='.')
         {
             cnt++;
             if(cnt>=k)
                ans++;
         }
         else cnt=0;
     }
    }
    }
    cout<<ans<<endl;
    return 0;
}

D.Substring

DP+拓扑排序

It is obvious that we can use dynamic programming algorithm to solve this stupid problem.

We can make an array f[i][j] to respect when you are at the point i, then how many letters j you can get. Note that i is ranging from 1 to n and j is from 1 to 26.

Then, you can do this dynamic programming algorithm by topological sorting. Specifically, you can use deg[i] to show how many edges that end at point i. First put all points i which satisfy deg[i] = 0 into a queue. When the queue is not empty, do the following steps repeatedly.

Take one point from the front of the queue. We say it is i.
Iterate all edges which begin at the point i. We say the endpoint of the edge is k. Then we update f[k][·] using f[i][·]. Finally we make deg[k] minus by 1. If deg[k] = 0, then we add the point k into the queue.
Make a variable cnt plus by 1.

When there is no cycle in the graph, the queue will be empty with cnt = n. Then the answer is the maximum number among f[i][j]. If there are cycles in the graph, then cnt cannot be n. Thus the answer can be arbitrarily large. In that situation, we should output -1.

Time complexity: 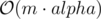$\text{[math]}$ , where alpha is the size of the alphabet (i.e. alpha = 26).

Memory complexity: 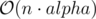$\text{[math]}$ .

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e5+5;
int n,m,cnt=0;
int dp[maxn][26],deg[maxn],head[maxn];
string a;
queue<int>q;
struct edge{
int to,nxt;
}e[maxn<<1];
void add(int u,int v)
{
    e[cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}
void topo()
{
    queue<int>q;
    for(int i=1;i<=n;i++)
    {
        if(!deg[i])
        {
          q.push(i);
          dp[i][a[i-1]-'a']++;
        }
    }
    int crt=0;
    while(!q.empty())
    {
       int u = q.front();q.pop();
       crt++;
       for(int i=head[u];~i;i=e[i].nxt)
       {
        int v=e[i].to;
        deg[v]--;
        if(!deg[v]) q.push(v);
        for(int j=0;j<26;j++)
            dp[v][j]=max(dp[v][j],dp[u][j]+(a[v-1]-'a'==j));
       }
    }
    if(crt<n) cout<<"-1"<<endl;
    else{
        int ans=0;
        for(int i=1;i<=n;i++)
            for(int j=0;j<26;j++)
             ans=max(ans,dp[i][j]);
        cout<<ans<<endl;
    }
}
int main()
{
   ios::sync_with_stdio(false);
   cin>>n>>m>>a;
   memset(head,-1,sizeof(head));
   memset(dp,0,sizeof(0));
   for(int i=0;i<m;i++)
   {
       int u,v;
       cin>>u>>v;
       add(u,v);
       deg[v]++;
   }
   topo();
   return 0;
}