组合数学中简单格路问题

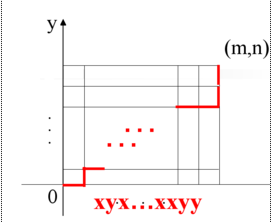
　　格路问题是较为经典的组合数学问题。问题主要内容是从(0,0)点出发沿x轴或y轴的正方向每步走一个单位，最终走到(m,n)点，求有多少条路径？

从(0,0)点出发到（m,n）点，无论怎么走，走的路径中，一定包含m个"-"和n个"|";其实观察发现无论"-"和"|"怎么组合，只要"-"个数够m个且"|"的个数

够n个，最终是一定能到达点(m,n)。

　　根据这个规律就可以将其转化成一个重排列问题。用b1表示"-",b2表示"|",那么这个问题就成为了求重集合{m.b1,n.b2}的全排列个数。

:

 

所以路径总数为：

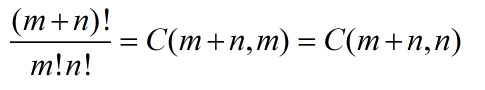
这是最基本的格路问题，其余的貌似都可以利用这种思想去分析。

 

 

转载于:https://www.cnblogs.com/wangkundentisy/p/5886896.html