S&p_15_极限定理

极限定理

1. 大数定律：随着试验次数的增大，这个频率趋于真实概率的可能性趋于1。

2. 中心定理：多重随机变量独立且服从0-1分布，当n趋向于无穷大是，多重随机变量联合分布服从正态分布。

3. 中心定理推广：多重随机变量独立同分布，当n趋向于无穷大是，多重随机变量联合分布服从正态分布。

中心极限定理代码：https://www.cnblogs.com/tlfox2006/p/10001242.html

 

1. 大数定律

引例 灯泡寿命估计

现有一批来自同一生产线的同型号 灯泡，每只灯泡的寿命服从相同的 分布，问任取一只灯泡，其寿命X 不低于1100小时的概率？

分析 寿命分布未知，P{X ≥1100}无法精确求得； 直观想法 测若干只灯泡的寿命，统计寿命不低于1100小时 的灯泡数量，求得频率f，用于近似概率P{X ≥1100}。

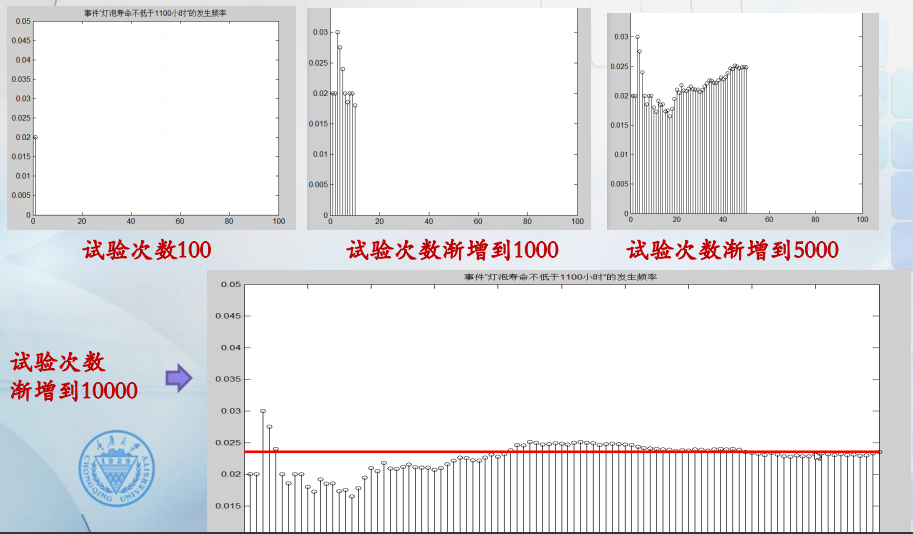
100次试验后，灯泡寿命不低于1100小时的发生概率为0.02...随着试验的次数增多，事件发生的频率趋向于时间发生的概率。

 

两个疑问 用“多次试验中事件发生的频率”去估计“一次试验事 件发生的概率”合理吗？

• ① 频率是否是稳定的？
• ② 频率是否是稳定到概率？

大数定律对这两个问题作出了肯定的回答，是频率稳定性的理论保证，大数定律是概率论中最著名的成果。

 

大数定律是有切比雪夫不等式推导而成，而切比雪夫不等式是由马尔科夫不等式推导而成。

 

 

马尔可夫不等式证明过程:

• 分段函数：x为非负函数，当0<x<a时，f(x)=0；当x>=a时，f(x)=a。
• 把x<a与x>=a分开证明，得出a×f(x) <= x
• 不等式两边去平均值（期望），最总得到P(x>=a) <= E(x)/a

  

 

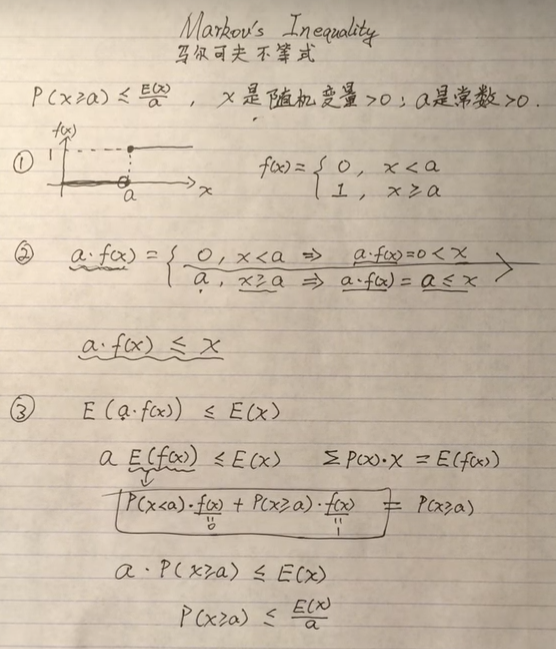
切比雪夫不等式： 利用方差来估计随机变量与它的数学期望的绝对偏差的一个概率估计数。其中x是随机数，μ是均值。x-μ的绝对值>=一个常数a的概率<=Var（x）/a²。

即若随机变量x的期望和方差都存在，x与μ的差

切比雪夫不等式证明过程：

• 若x是一个随机数，则x减去一个常数，同样得到也是一个随机数。
• 证明P(|x-μ|>=a) 等于 P((x-μ)²>=a²). 
  • {x>=a+μ or x<=-a+μ}的意思是x是落在阴影部分。即有50%的概率{|x-μ|>=a}是成立的，所以|x-μ|>=a的概率等于{x>=a+μ or x<=-a+μ}的概率。
  • 同理，证明出(x-μ)²>=a²的概率等于{x>=a+μ or x<=-a+μ}的概率。
  • 综上2点，的得到P(|x-μ|>=a) 等于 P((x-μ)²>=a²)
• 将X=x-μ代入马尔可夫不等式，得出P(|x-μ|>=a) <= Var（x）/a²，即切比雪夫不等式。 

 

 

大数定律：

 

回到引例

引例中，通过试验模拟，得到灯泡寿命不低于1100小 时的频率逐渐稳定在0.0235 左右，由强大数定律，结论“ 任取一只灯泡，其寿命不低于1100小时的概率P{X ≥1100}= 0.0235 ”是合理的，随着试验次数的增大，这个频率趋于真实概率的可能性趋于1。

 

2. 中心极限定理

引问：为什么世界上的大多数分布服从正太分布？

其内在原因就是随机现象背后中心极限定理的存在。

 

正态分布：

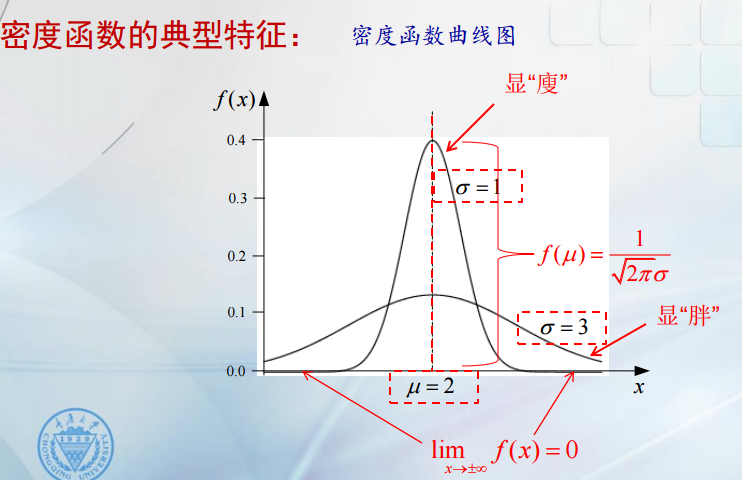
正太分布的密度函数的典型特征：

• μ是曲线的对称点，它决定曲线的中心位置，称为位置参数。
• 函数f(x)在μ处达到最大值。f(μ)=1/(2∏*σ)^0.5
• 参数σ值越小，曲线显瘦，反之曲线显胖。称参数σ为形状参数。
• 当x趋于+-无穷时，limf(x)=0。
• 当μ=0，σ=1时，函数分布为标准正态分布。

 

多重随机变量独立且服从0-1分布，当n趋向于无穷大是，多重随机变量联合分布服从正态分布。

 

引例一 炮弹落点误差问题?

 炮弹落点误差的因素有多个，如士兵瞄准误差，空气阻力误差等等。求多重随机变量的和分布：

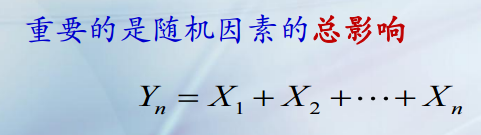
所以Yn服从正态分布。

 

中心极限定理推广

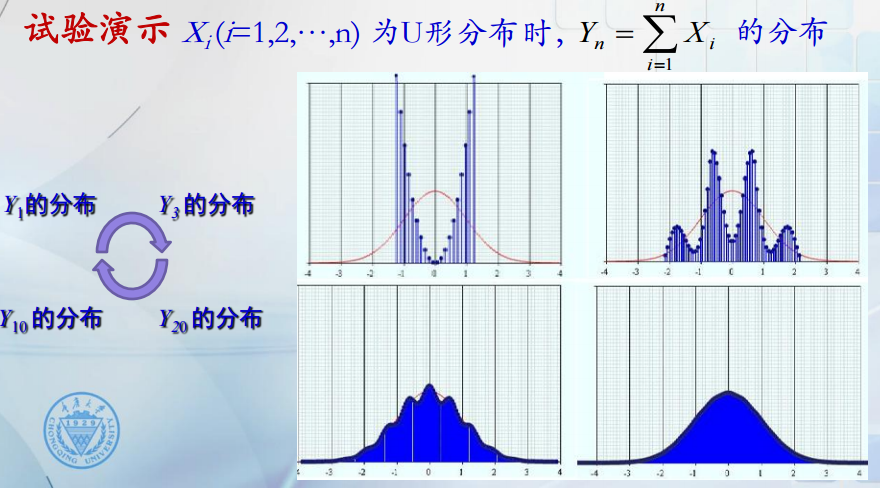
若X1 ,X2 ,…,Xn ,…独立同分布，但不是0-1分布时，Yn服从什么分布？

如图所示，随着随机变量的增多，联合分布会趋向于正态分布。

  

 

 

转载于:https://www.cnblogs.com/tlfox2006/p/9989520.html