查找算法

最新推荐文章于 2024-10-11 10:58:10 发布

转载最新推荐文章于 2024-10-11 10:58:10 发布 · 61 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/xiao-apple36/p/8457473.html

本文介绍了两种基本的查找算法——列表查找与二分查找。列表查找通过遍历整个列表来寻找目标元素；二分查找则针对有序列表，通过不断缩小候选区域来提高查找效率。实测显示，对于大数据集，二分查找远优于列表查找。

列表查找（线性表查找）：从列表中查找指定元素

算法描述

从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。
输入：列表、待查找元素
输出：元素下标（未找到元素时一般返回None或一1）
内置列表查找函数：index()

代码实现

# 线性查找 时间复杂度o(n)
@cal_time
def linear_search(li, val):
    for ind, v in enumerate(li):
        if v == val:
            return ind
    else:
        return -1

# 计算时间
def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.clock() # 类unix平台使用time.time()
        result = func(*args, **kwargs)
        t2 = time.clock() # 类unix平台使用time.time()
        print('%s running time: %20.12f secs.'%(func.__name__,(t2-t1)))
        return result
    return wrapper

二分查找（折半查找）：从有序列表候选区开始，每次把查找的值与候选区中间值进行比较。

算法示意图（每次查找比较后，可以使候选区减少一半）

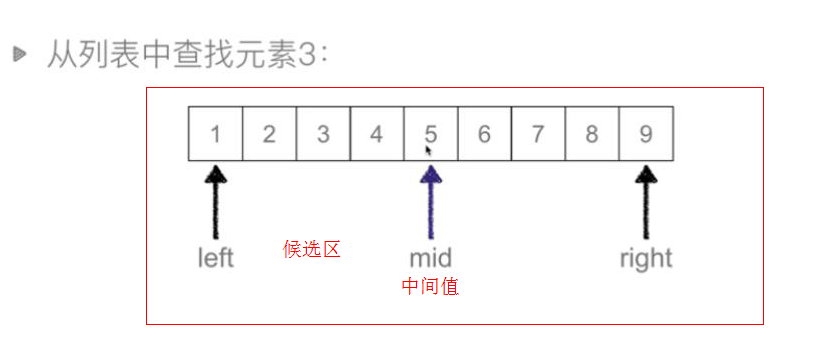
中间值5>3,说明需要找的值在中间值左边。

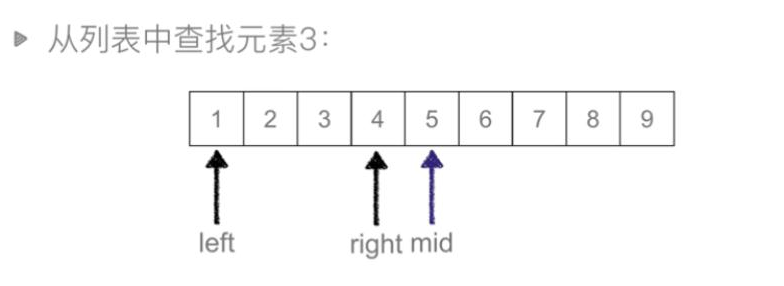
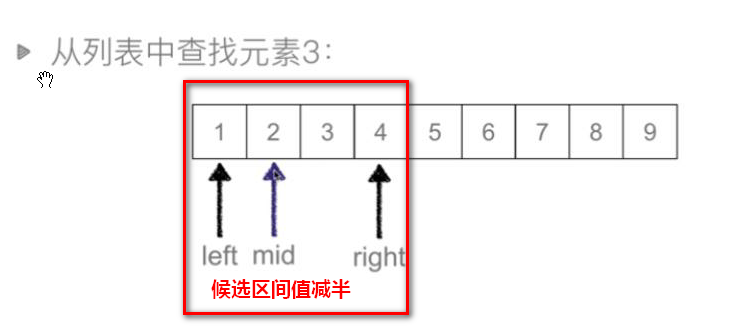
取mid=2,待查找元素3>2,说明需要找的值在中间值右边。

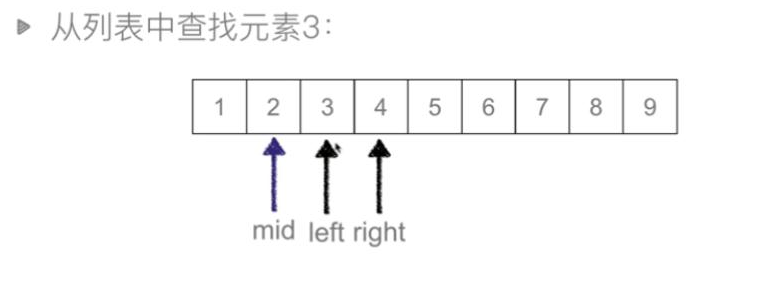
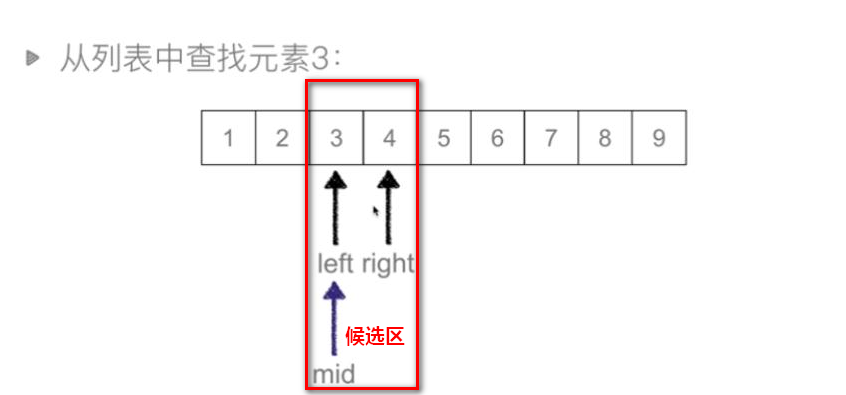
取mid=3,待查找元素3=3，查找成功。如果待查找元素不存在，当right<left结束查找。

代码实现

# 折半查找 复杂度o(log n)
@cal_time
def binary_search(li, val):
    left = 0
    right = len(li)-1
    while left <= right: # 候选区间
        mid = (left + right) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val: # 待查找的值在mid的左边
            right = mid - 1
        else: # li[mid] < val 待查找的值在mid的右边
            left = mid + 1
    else:
        return -1

算法效率比较

if __name__ == '__main__':
    li = [i for i in range(100,100000000)]
    binary_search(li, 398222222)
    linear_search(li, 398002222)


>>>>>运行结果
binary_search running time:      0.000018193752 secs.
linear_search running time:      6.288672803093 secs.

转载于:https://www.cnblogs.com/xiao-apple36/p/8457473.html