VMware Coding Challenge: The Heist

weixin_30709061

于 2015-03-07 03:50:00 发布

阅读量56

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/EdwardLiu/p/4319664.html

本文探讨了如何解决Backpack II问题，并通过实例代码详细解释了解决过程。重点介绍了算法设计、动态规划方法的应用以及如何优化解决方案。

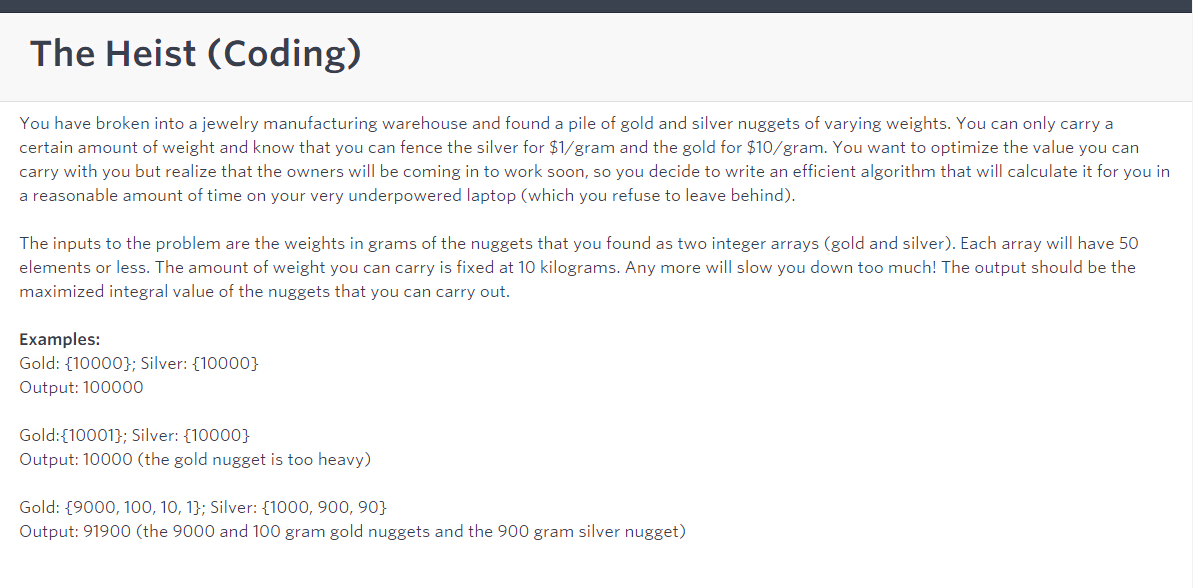
类似BackpackII问题

 1     static int maximize_loot(int[] gold, int[] silver) {
 2         int[][] res = new int[gold.length+silver.length+1][10001];
 3         res[0][0] = 0;
 4         for (int i=1; i<=gold.length; i++) {
 5             for (int j=0; j<=10000; j++) {
 6                 res[i][j] = Math.max(res[i-1][j], (j>=gold[i-1]? res[i-1][j-gold[i-1]]+10*gold[i-1] : 0));
 7             }
 8         }
 9         for (int i=1; i<=silver.length; i++) {
10             for (int j=0; j<=10000; j++) {
11                 res[i+gold.length][j] = Math.max(res[i+gold.length-1][j], (j>=silver[i-1]? res[i+gold.length-1][j-silver[i-1]]+1*silver[i-1] : 0));
12             }
13         }
14         int maxVal = 0;
15         for (int k=0; k<=10000; k++) {
16             maxVal = Math.max(maxVal, res[gold.length+silver.length][k]);
17         }
18         return maxVal;
19 
20     }