一些常用算法

区间查询问题：

1.RMQ

一般通过预处理实现O(1)的查询时间

最普通的：rmq[i][j](0<=i<=j<length(A))，rmq[i][j] = min(rmq[i][j-1], A[j])，复杂度O(n^2)

用Sparse Table：rmq[i][j]，覆盖区间(i, i+2^j-1)，查询时Q(m, n)组合两个区间(可覆盖)，从m开始向左的一段区间，和从n开始向右的一段区间（[m, m+2^k-1]， [n-2^k+1, n]），即为min(rmq[m][k], rmq[n-2^k+1][k])。

ST方法中rmq[i][j](i + (1<<j) - 1 < n) = rmq[i][j-1], rmq[i+2^(j-1)][j-1]。复杂度O(nlogn)。

标准RMQ算法：

2.线段树

注意节点保存的信息，以及lazy更新。一些几何问题先离散化处理。

3.树状数组

 

字符串处理：

TRIE树：

TRIE图：

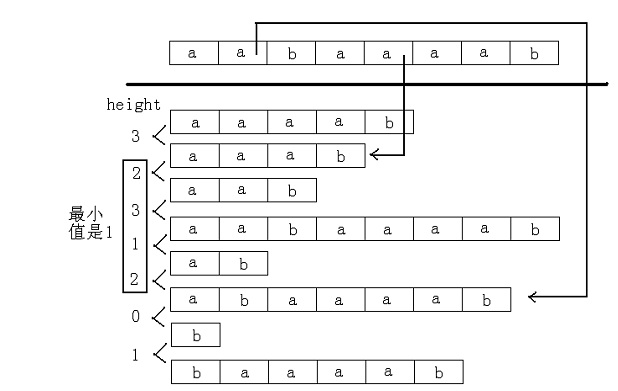
后缀数组：SA数组，rank数组，height数组

 

网络流：

最大流：EK算法

最小费用最大流：类似FF算法，dijkstra或spfa在残量网络找到费用权值增广路。

 

 

 

 

 

 

 

 

 

 

 

转载于:https://www.cnblogs.com/fenglei2012/p/3355686.html