第一次作业

1-1 数据压缩的一个基本问题是“我们要压缩什么”，对此你是怎么理解的？

 

答：数据压缩的对象即信号空间，指的是物理空间、时间区间和电磁频段，也就是指某信号集合所占的空域、时域和频域空间。

 

1-2 数据压缩的另一个基本问题是“为什么进行压缩”，对此你又是怎么理解的？

 

答：进行数据压缩可以：1、较快地传输各种信源（降低新到占有费用）；2、在现有信息干线上开通更多的并行业务；3、降低发射功率；4、紧缩数据存储容量。

 

1-6 数据压缩技术是如何分类的？

 

答：数据压缩分为在某种程度上可逆的与实际上不可逆的两大类。

 

 Page 8  1.4项目与习题

1、用你的计算机上的压缩工具来压缩不同文件。研究原文件的大小和类型对于压缩文件与原文件大小之比的影响。

 

答：我在使用我自己的计算机上的压缩工具压缩不同文件之后发现，不同文件压缩之后的压缩比是不一样的。相对来说，视频和音频文件的压缩比是比较小的。

 

2、从一本通俗杂志中摘录几段文字，并删除所有不会影响理解的文字，实现压缩。例如，在"this is the dog that belong to my friend”  中，删除 is 、the、that和to之后，仍然能传递相同的意思。用被删除的单词数与原文本的总单词数之比来衡量文本中的冗余度。用一本技术期刊中的文字来重复这一实验。对于摘自不同来源的文字，我们能否就其冗余度做出定量论述？

 

答：不能对摘自不同来源的文字的冗余度做定量论述，对于不同的信息来说，重复度是不一样的。

 

Page 30

3、给定符号集A={a₁,a₂,a₃,a₄},求一下条件下的一阶熵：

（a）P(a₁)=P(a₂)=P(a₃)=P(a₄)=1/4

（b）P(a₁)=1/2 , P(a₂)=1/4 , P(a₃)=P(a₄)=1/8 

（c）P(a₁)=0.505 ,  P(a₂)=1/4 , P(a₃)=1/8 , P(a₄)=0.12 

答： (a) H=2bit

       (b)  H=0.5+0.5+0.375+0.375=1.75bit

       (c) H=0.5+0.5+0.375+0.367=1.742bit

 

5、考虑以下序列：

                       ATGCTTAACGTGCTTAACCTGAAGCTTCCGCTGAAGAACCTG

                       CTGAACCCGCTTAAGCTTAAGCTGAACCTTCTGAACCTGCTT

（a）根据此序列估计个概率值，并计算这一序列的一阶、二阶、三阶和四阶熵。

（b）根据这些熵，能否推断此序列具有什么样的结构？

答：(a)一阶为：

P(A)=21/84=1/4 、P(G)=16/84=4/21 、P(C)=24/84=2/7、P(T)=23/84

H=2

 

7、做一个实验，看看一个模型能够多么准确地描述一个信源

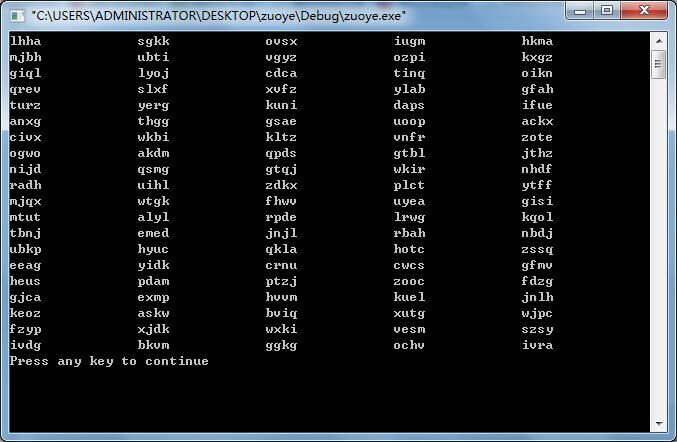
(a)编写一段程序，从包括26个字母的符号集{a,b,...,z}中随机选择字母，组成100个四字母单词，这些单词中有多少是有意义的？

答：

#include<stdio.h>
#include <stdlib.h>
#include<time.h>
int main()
{
char a[200][200];
int b;
srand((int)time(NULL));
for(int i=1;i<=100;i++)
{
for(int j=1;j<=4;j++)
{

b=rand()%26;
a[i][j]=b+'a';
}
}

for( i=1;i<=100;i++)
{
for(int j=1;j<=4;j++)
{
printf("%c",a[i][j]);
}
printf("\t\t");
}

return 0;
}

转载于:https://www.cnblogs.com/yuruogu/p/4765805.html