Trapezoidal Shadow Map(1)

最新推荐文章于 2019-12-31 14:11:56 发布

weixin_30697239

最新推荐文章于 2019-12-31 14:11:56 发布

阅读量156

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/sevecol/archive/2005/08/03/206136.html

博客介绍了在light’s post−perspective space中根据视锥构建的梯形，用贴图表示相关参数。重点展示了从light’s post−perspective space到trapezoidal space的矩阵计算过程，包含平移、旋转、变换等多个步骤。

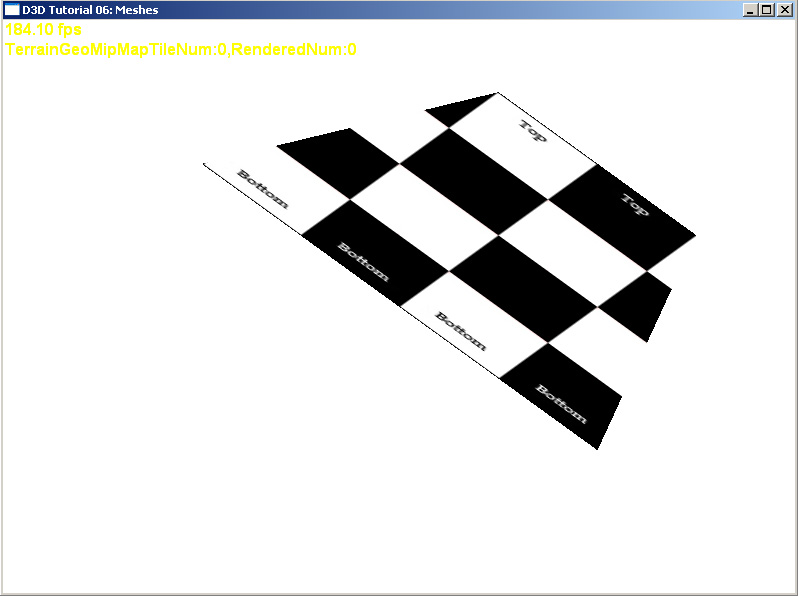
在light’s post−perspective space中根据视锥构建的梯形,为了方便表示,贴了一张贴图表示.贴图中的Top表示靠近视锥前截面的梯形的上底,Bottom表示靠近视锥后截面的梯形的下底.

梯形转换到trapezoidal space后的显示情况

light’s post−perspective space->trapezoidal space的距阵计算:

HRESULT CTrapezoidalShadowMap::ComputeTrapezoidalMatrix(D3DXMATRIX& matrix,D3DXVECTOR3& topl,D3DXVECTOR3& topr,D3DXVECTOR3& bottoml,D3DXVECTOR3& bottomr,D3DXVECTOR3& intersection)
{
// 平移TopLine的中点到Light's Post-Perspective Space的中点
D3DXMatrixTranslation(&matrix,-(topl.x+topr.x)/2.0f,-(topl.y+topr.y)/2.0f,0);

// 旋转梯形使得TopLine和Light's Post-Perspective Space的x轴重合
D3DXVECTOR3 t_topline=(topl-topr);
D3DXVec3Normalize(&t_topline,&t_topline);

float t_angle=D3DXVec3Dot(&t_topline,&D3DXVECTOR3(1,0,0));

D3DXMATRIX t_matrix;
D3DXMatrixRotationZ(&t_matrix,-acosf(t_angle));

matrix*=t_matrix;

// 平移梯形使得两侧边交点到Light's Post-Perspective Space的中点
D3DXVECTOR3 t_intersection;

D3DXVec3TransformCoord(&t_intersection,&intersection,&matrix);

D3DXMatrixTranslation(&t_matrix,-t_intersection.x,-t_intersection.y,0);

matrix*=t_matrix;

// 变换使得成为等边梯形
D3DXVECTOR3 t_point1,t_point2;
D3DXVec3TransformCoord(&t_point1,&topl,&matrix);
D3DXVec3TransformCoord(&t_point2,&topr,&matrix);

t_point1+=t_point2;

D3DXMatrixIdentity(&t_matrix);
t_matrix._21=-t_point1.x/t_point1.y;

matrix*=t_matrix;

// 变换使得两侧边成90度,TopLine的两点在[-1,1]和[1,1]上
D3DXVec3TransformCoord(&t_point1,&topr,&matrix);

D3DXMatrixScaling(&t_matrix,1.0f/t_point1.x,1.0f/t_point1.y,1.0f);

matrix*=t_matrix;

// 变换使得梯形变成矩形
t_matrix._11=t_matrix._22=t_matrix._33=t_matrix._24=t_matrix._42=1.0f;
t_matrix._12=t_matrix._13=t_matrix._14=t_matrix._21=t_matrix._23=0.0f;
t_matrix._31=t_matrix._32=t_matrix._34=t_matrix._41=t_matrix._43=t_matrix._44=0.0f;

matrix*=t_matrix;

// 平移使得矩形的中心到Light's Post-Perspective Space的中点
D3DXVec3TransformCoord(&t_point1,&topl,&matrix);
D3DXVec3TransformCoord(&t_point2,&bottomr,&matrix);

D3DXMatrixTranslation(&t_matrix,0,-(t_point1.y+t_point2.y)/2.0f,0);

matrix*=t_matrix;

// 拉伸矩形的Y方向,使得充满整个Light's Post-Perspective Space
D3DXVECTOR4 t_point3;
D3DXVec3Transform(&t_point3,&topl,&matrix);

D3DXMatrixIdentity(&t_matrix);

t_matrix._22=-t_point3.w/t_point3.y;

matrix*=t_matrix;

//
return S_OK;
};

转载于:https://www.cnblogs.com/sevecol/archive/2005/08/03/206136.html