第四篇 栈与队列（一）

一、栈的定义

栈是限定仅在表尾进行插入和删除操作的线性表；栈又称为后进先出的线性表（LIFO）。

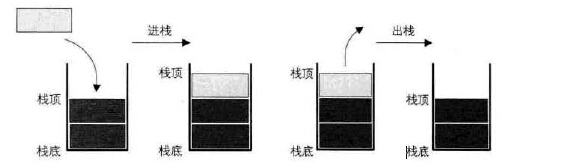
栈顶：允许插入和删除操作的一端称为栈顶；而另一端则为栈底。

栈的操作：插入数据称为进栈（压栈、入栈）；栈的删除操作称为出栈（弹栈）。

如下图所示：

　　　　　　

二、栈的抽象数据类型

　　　　栈是一种特殊的线性表，因此具有线性表的所有特性。如除根节点以外，有且仅有一个前驱节点等。

　　　　

三、栈的顺序存储结构及实现

C#代码实现

    /// <summary>
    /// 栈的顺序存储结构
    /// </summary>
    /// <typeparam name="T"></typeparam>
    public class SequenceStoregeStackt<T>
    {
        //栈的最大空间
        private int _maxSize;

        //栈顶指针
        private int _top;

        //栈的数据用数据进行存储
        private T[] _storage;

        public SequenceStoregeStackt(int maxSize)
        {
            _maxSize = maxSize;

            _storage = new T[maxSize];
        }

        /// <summary>
        /// 判断栈是否为空
        /// </summary>
        /// <returns></returns>
        public bool IsEmpty()
        {
            return _top == -1;
        }

        /// <summary>
        /// 添加元素
        /// 栈只能从栈顶添加元素
        /// </summary>
        /// <param name="t">添加的元素</param>
        public void Push(T t)
        {
            if (_top == _maxSize - 1)
                throw new ApplicationException("The stack is full.");
            //将元素添加到栈顶
            _storage[_top + 1] = t;

            //将栈顶指针+1
            _top++;
        }

        /// <summary>
        /// 取出栈顶元素
        /// </summary>
        public T Pop()
        {
            T t = default(T);
            if (!IsEmpty())
            {
                t = _storage[_top];
                _top--;
            }
            return t;
        }
    }

　四、栈的链式存储结构

　　C#代码实现

    /// <summary>
    /// 栈的链式结构实现
    /// </summary>
    public class LinkedStack<T>
    {
        /// <summary>
        /// 栈的指针
        /// </summary>
        private Node<T> _top;

        /// <summary>
        /// 栈的长度
        /// </summary>
        public int Length { get; set; }

        public LinkedStack()
        {

        }

        /// <summary>
        /// 判断栈是否为空
        /// </summary>
        /// <returns></returns>
        public bool IsEmpty()
        {
            return _top == null;
        }

        /// <summary>
        /// 插入元素
        /// </summary>
        /// <param name="t"></param>
        public void Push(T t)
        {
            //栈的连式存储只有在内存满了，才会添加失败
            Node<T> node = new Node<T>();
            node.t = t;
            //将当前的栈顶元素赋值给新节点的直接后继
            node.NextNode = _top;
            //将新的节点赋给栈顶指针
            _top = node;
            //将栈的长度+1
            Length++;
        }

        /// <summary>
        /// 取出栈顶元素
        /// </summary>
        /// <returns></returns>
        public T Pop()
        {
            T t = default(T);
            if (!IsEmpty())
            {
                //取得栈顶元素
                Node<T> node = _top;
                //取得值
                t = node.t;
                //修改栈顶指针
                _top = _top.NextNode;
                //修改栈长度
                Length--;
            }
            return t;
        }
    }

    /// <summary>
    /// 栈的元素
    /// </summary>
    /// <typeparam name="T"></typeparam>
    public class Node<T>
    {
        /// <summary>
        /// 栈的数据元素
        /// </summary>
        public T t { get; set; }

        /// <summary>
        /// 下一节点指针
        /// </summary>
        public Node<T> NextNode { get; set; }
    }

　五、栈的应用之递归

　　斐波那契数列【具体解释参考百度百科】

　　斐波那契数列数学表示：

　　

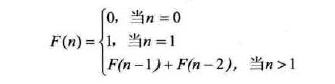
　　C#代码实现

　　

  /// <summary>
    /// 斐波那契数列实现
    /// </summary>
    public class FibonacciDemo
    {
        /// <summary>
        /// 递归实现
        /// </summary>
        /// <param name="value">输入的数列项</param>
        /// <returns></returns>
        public int Execute(int value)
        {
            if (value < 2)
                return 1;
            return Execute(value - 1) + Execute(value - 2);
        }

        /// <summary>
        /// 斐波那契的循环实现
        /// </summary>
        /// <param name="value"></param>
        /// <returns></returns>
        public int LoopExecute(int value)
        {
            int[] arr = new int[value];
            if (value == 0)
                return 0;
            if (value == 1)
                return 1;
            int sum = 0;
            arr[0] = 0;
            arr[1] = 1;
            for (int i = 2; i < value; i++)
            {
                int temp = arr[i - 1] + arr[i - 2];
                sum = sum + temp;
            }
            return sum;
        }
    }

　六、栈的应用之四则运算

　　后缀表达式（逆波兰）

 

转载于:https://www.cnblogs.com/xiuyuanjing/p/4133914.html