题目描述
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
解题思路:得到f(n)=f(n-1)+f(n-2)

1 #include <iostream> 2 using namespace std; 3 class Solution { 4 public: 5 //fn=f(n-1)+f(n-2) 6 int rectCover(int number) { 7 int result[3]={0,1,2}; 8 if(number<=2) 9 return result[number]; 10 int f1 = 1; 11 int f2 = 2; 12 int fn = 0; 13 for(int i=3;i<=number;i++) 14 { 15 fn = f1 + f2; 16 f1 = f2; 17 f2 = fn; 18 } 19 return fn; 20 } 21 }; 22 int main() 23 { 24 int n; 25 while(cin>>n) 26 { 27 Solution s; 28 cout<<"1*2小矩形放入2*"<<n<<"大矩形中有"<<s.rectCover(n)<<"种放法"<<endl; 29 } 30 return 0; 31 }
输出结果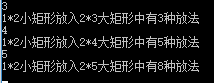




 本文探讨了使用2*1小矩形无重叠覆盖2*n大矩形的方法总数问题。通过递推公式f(n)=f(n-1)+f(n-2)实现高效求解,并提供了完整的C++代码实现。
本文探讨了使用2*1小矩形无重叠覆盖2*n大矩形的方法总数问题。通过递推公式f(n)=f(n-1)+f(n-2)实现高效求解,并提供了完整的C++代码实现。
















 146
146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








