本文解析了NOIP2016的三道题目，包括签到题、换教室和天天爱跑步，涉及模拟算法、期望DP和树上差分等技术，提供了详细的代码实现。
T1
签到题，简单的模拟，只要水平还行就能随便A吧
毕竟当年我那么菜都A掉了这道题
2年前的代码风格，勿喷orz
1 #include<iostream> 2 #include<stdio.h> 3 #include<cstdio> 4 #include<string.h> 5 #include<algorithm> 6 #include<cmath> 7 #include<cstring> 8 #include<string> 9 using namespace std; 10 struct wj 11 { 12 int x,xx,yy; 13 string ss; 14 }num[100005],order[100005]; 15 char ss[100006][11]; 16 int m,n; 17 int main() 18 { 19 cin>>n>>m; 20 for(int i=1;i<=n;i++) 21 { 22 cin>>num[i].x; 23 scanf("%s",&ss[i]); 24 } 25 int ans=1; 26 int qq; 27 for(int i=1;i<=m;i++) 28 { 29 cin>>order[i].xx>>order[i].yy; 30 if(num[ans].x==order[i].xx) 31 { 32 ans-=order[i].yy; 33 } 34 else 35 { 36 ans+=order[i].yy; 37 } 38 while(ans<=0)ans=ans+n; 39 while(ans>n)ans=ans-n; 40 } 41 for(int i=0;i<=10;i++) 42 cout<<ss[ans][i]; 43 return 0; 44 }
T3
那个时候我连Floyd都不会（笑）
其实就是一道阅读理解题，读懂题面的话显然这道题是期望DP，理论上是随便A的，只是DP式比较长
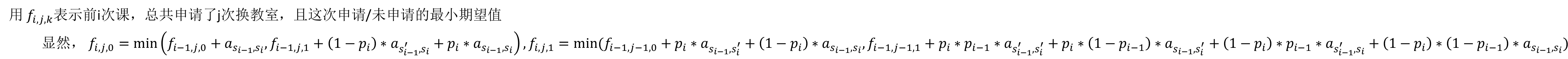
码力不差，而且知道期望DP怎么写的应该都可以A吧
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 #include<cstdlib> 6 #include<cctype> 7 using std::cin; 8 using std::cout; 9 using std::endl; 10 int a[310][310], n, m, v, c[2010], d[2010], e; 11 double f[2010][2010][2], p[2010]; 12 int read() { 13 int x = 0, y = 1; 14 char ch = getchar(); 15 while (!isdigit(ch)) { 16 if (ch == '-') y = -1; 17 ch = getchar(); 18 } 19 while (isdigit(ch)) { 20 x = (x << 1) + (x << 3) + ch - '0'; 21 ch = getchar(); 22 } 23 return x * y; 24 } 25 26 void init() { 27 n = read(); m = read(); v = read(); e = read(); 28 memset(a, 0x3f, sizeof(a)); 29 for (int i = 1; i <= n; i++) c[i] = read(); 30 for (int i = 1; i <= n; i++) d[i] = read(); 31 for (int i = 1; i <= n; i++) scanf("%lf", &p[i]); 32 while (e--) { 33 int x = read(), y = read(); 34 a[x][y] = std::min(a[x][y], read()); 35 a[y][x] = a[x][y]; 36 } 37 } 38 39 void floyd() { 40 for (int i = 1; i <= v; i++) a[i][i] = 0; 41 for (int k = 1; k <= v; k++) 42 for (int i = 1; i <= v; i++) 43 for (int j = 1; j <= v; j++) a[i][j] = std::min(a[i][j], a[i][k] + a[k][j]); 44 } 45 46 void work() { 47 for (int i = 1; i <= n; i++) 48 for (int j = 0; j <= m; j++) f[i][j][0] = f[i][j][1] = 1e9; 49 f[1][1][1] = f[1][0][0] = 0; 50 for (int i = 2; i <= n; i++) { 51 f[i][0][0] = f[i - 1][0][0] + a[c[i - 1]][c[i]]; 52 f[i][0][1] = 1e9; 53 for (int j = 1; j <= ((m < i) ? m : i); j++) { 54 f[i][j][0] = std::min(f[i - 1][j][0] + a[c[i - 1]][c[i]], f[i - 1][j][1] + p[i - 1] * a[d[i - 1]][c[i]] + (1 - p[i - 1]) * a[c[i - 1]][c[i]]); 55 f[i][j][1] = std::min(f[i - 1][j - 1][0] + p[i] * (a[c[i - 1]][d[i]]) + (1 - p[i]) * a[c[i - 1]][c[i]], f[i - 1][j - 1][1] + p[i - 1] * p[i] * a[d[i - 1]][d[i]] + p[i - 1] * (1 - p[i]) * a[d[i - 1]][c[i]] + (1 - p[i - 1]) * p[i] * a[c[i - 1]][d[i]] + (1 - p[i - 1]) * (1 - p[i]) * a[c[i - 1]][c[i]]); 56 } 57 } 58 double min = 1e9; 59 for (int i = 0; i <= m; i++) min = std::min(min, std::min(f[n][i][0], f[n][i][1])); 60 printf("%.2lf\n", min); 61 } 62 63 int main() { 64 init(); 65 floyd(); 66 work(); 67 return 0; 68 }
T2
个人觉得是NOIP2016思维难度最高的一道题，不过因为 T1 和 T3 较水，水平还行的话现场65分还是可做的
暴力的做法当然是对于每条路径做一次DFS，时间复杂度 O(n2)，大概只有25分
对于 Si=1 的情况，显然路径只对 depth[i] == w[i] 的点有贡献，把所有终点的值标为1然后求子树和即可
对于 Ti=1 的情况，显然只有子树上的 depth[u[i]] == w[i] + d[i] 的情况才对当前点有贡献，DFS序列化+主席树大概可以解决，更优的做法在正解中会提到
对于 n 与 n-1 有边的情况，显然这道题变成了区间问题，假如 u[i] < =v[i]，显然这条路径只对 u[i] == x - w[x] 的点产生贡献，加入 u[i] > v[i]，显然这条路径只对 u[i] == x + w[x] 的点产生贡献，u[i] 是个定值，很容易联想到差分，用 sum[i] 记录走到当前点的时候还有多少条从 i 出发的路径，在 u[i] 和 v[i] 处分别打上 +1 和 -1 标记即可
以上几组特殊情况显然是在暗示正解。从 u[i] 出发到 v[i] 的路径显然可以拆分成两条路径，一条从 u[i] 到 lca[i]，另一条从 lca[i] 到 v[i]，显然对于前者，这条路径只对 depth[u[i]] == depth[x] + w[x] 的点产生贡献，对于后者，这条路径只对 depth[u[i]] - 2 * depth[lca[i]] + depth[x] == w[x] 的点产生贡献，移项得：depth[u[i]] - 2 * depth[lca[i]] == w[x] - depth[x]，这两个等式的左边都是定值，结合 n 与 n-1 有边的特殊情况，可以用树上差分的方法解决这个问题，不过拆分成两条路径之后，如果 lca[i] 满足一个等式的条件，另外一个等式的条件也一定可以满足，因此对于这种条件我们多计算了一次，把它减掉即可
1 #include<bits/stdc++.h> 2 using std::vector; 3 using std::cin; 4 using std::cout; 5 using std::streambuf; 6 //define 7 #define MAXN 300000 8 #define MAXM 600000 9 #define D 10 10 #define UP(i, l, r) for (int i = l; i <= r; ++i) 11 #define DOWN(i, l, r) for (int i = r; i >= l; --i) 12 #define AUTO(i, x) for (int i = graph::lin[x]; i; i = edge[i].ne) 13 //input 14 namespace IN { 15 #define MAX_INPUT 10000000 16 #define cinchar() (fs == ft ? (ft = (fs = buf) + fb -> sgetn(buf, MAX_INPUT), fs == ft ? 0 : *fs++) : *fs++) 17 char *fs, *ft, buf[MAX_INPUT]; 18 inline int read() { 19 int x = 0; 20 streambuf *fb = cin.rdbuf(); 21 char ch = cinchar(); 22 while (!isdigit(ch)) ch = cinchar(); 23 while (isdigit(ch)) { 24 x = x * 10 + ch - '0'; 25 ch = cinchar(); 26 } 27 return x; 28 } 29 #undef MAX_INPUT 30 #undef cinchar 31 } 32 using IN::read; 33 34 //output 35 namespace OUT { 36 int top = 0; 37 char buf[11]; 38 inline void put(int x, int opt) { 39 streambuf *fb = cout.rdbuf(); 40 if (!x) { 41 fb -> sputc('0'); fb -> sputc(opt); 42 return; 43 } 44 if (x < 0) { 45 x = -x; 46 fb -> sputc('-'); 47 } 48 while (x) { 49 buf[++top] = x % 10 + '0'; 50 x /= 10; 51 } 52 while (top) fb -> sputc(buf[top--]); 53 fb -> sputc(opt); 54 } 55 } 56 using OUT::put; 57 58 //graph 59 namespace graph { 60 int len = 0, lin[MAXN + D]; 61 struct node { 62 int y, ne; 63 } edge[MAXM + D]; 64 inline void addedge(int x, int y) { 65 edge[++len].y = y; edge[len].ne = lin[x]; lin[x] = len; 66 } 67 } 68 using graph::edge; 69 using graph::addedge; 70 71 //query 72 namespace query { 73 int len = 0, lin[MAXN + D]; 74 struct query{ 75 int y, ne, id; 76 } q[MAXM + D]; 77 inline void addquery(int x, int y, int id) { 78 q[++len].y = y; q[len].id = id; q[len].ne = lin[x]; lin[x] = len; 79 } 80 } 81 using query::q; 82 using query::addquery; 83 84 int n, m, depth[MAXN + D], u[MAXN + D], v[MAXN + D], lca[MAXN + D], sum[MAXM + D], w[MAXN + D], ans[MAXN + D]; 85 vector<int> tag_add[MAXN + D], tag_del[MAXN + D]; 86 87 namespace tarjan { 88 int father[MAXN + D]; 89 bool vis[MAXN + D]; 90 inline int getfather(int x) { 91 int ancesstor = x, tmp; 92 while (ancesstor != father[ancesstor]) ancesstor = father[ancesstor]; 93 while (x != ancesstor) { 94 tmp = father[x]; 95 father[x] = ancesstor; 96 x = tmp; 97 } 98 return ancesstor; 99 } 100 101 void reset() { 102 UP(i, 1, n) father[i] = i; 103 } 104 105 void dfs(int x, int par = 0) { 106 vis[x] = true; 107 AUTO(i, x) { 108 int y = edge[i].y; 109 if (y == par) continue; 110 depth[y] = depth[x] + 1; 111 dfs(y, x); 112 father[y] = x; 113 } 114 for (int i = query::lin[x], y; i; i = q[i].ne) if (vis[y = q[i].y]) lca[q[i].id] = getfather(y); 115 } 116 } 117 using tarjan::reset; 118 119 void init() { 120 n = read(); m = read(); 121 UP(i, 1, n - 1) { 122 int x = read(), y = read(); 123 addedge(x, y); addedge(y, x); 124 } 125 UP(i, 1, n) w[i] = read(); 126 UP(i, 1, m) { 127 u[i] = read(); v[i] = read(); 128 addquery(u[i], v[i], i); 129 addquery(v[i], u[i], i); 130 } 131 } 132 133 void dfs(int x, int par) { 134 int backup = sum[depth[x] + w[x] + MAXN]; 135 AUTO(i, x) { 136 int y = edge[i].y; 137 if (y == par) continue; 138 dfs(y, x); 139 } 140 for (int i = 0; i < tag_add[x].size(); ++i) ++sum[tag_add[x][i]]; 141 ans[x] = sum[w[x] + depth[x] + MAXN] - backup; 142 for (int i = 0; i < tag_del[x].size(); ++i) --sum[tag_del[x][i]]; 143 } 144 145 void DFS(int x, int par) { 146 int backup = sum[w[x] - depth[x] + MAXN]; 147 AUTO(i, x) { 148 int y = edge[i].y; 149 if (y == par) continue; 150 DFS(y, x); 151 } 152 for (int i = 0; i < tag_add[x].size(); ++i) ++sum[tag_add[x][i]]; 153 ans[x] += sum[w[x] - depth[x] + MAXN] - backup; 154 for (int i = 0; i < tag_del[x].size(); ++i) --sum[tag_del[x][i]]; 155 } 156 157 void solve() { 158 reset(); 159 depth[1] = 0; 160 tarjan::dfs(1); 161 UP(i, 1, m) { 162 tag_add[u[i]].push_back(depth[u[i]] + MAXN); 163 tag_del[lca[i]].push_back(depth[u[i]] + MAXN); 164 } 165 dfs(1, 0); 166 UP(i, 1, n) { 167 vector<int>().swap(tag_add[i]); vector<int>().swap(tag_del[i]); 168 } 169 UP(i, 1, m) { 170 tag_add[v[i]].push_back(depth[u[i]] - (depth[lca[i]] << 1) + MAXN); 171 tag_del[lca[i]].push_back(depth[u[i]] - (depth[lca[i]] << 1) + MAXN); 172 } 173 DFS(1, 0); 174 UP(i, 1, m) if (depth[u[i]] - depth[lca[i]] == w[lca[i]]) --ans[lca[i]]; 175 } 176 177 int main() { 178 std::ios::sync_with_stdio(false); 179 cin.tie(NULL); cout.tie(NULL); 180 init(); 181 solve(); 182 UP(i, 1, n - 1) put(ans[i], ' '); 183 put(ans[n], '\n'); 184 return 0; 185 }
扫一扫
948
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
