【贪心】「poj1328」Radar Installation

建模：二维转一维；贪心

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d. 

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates. 
 
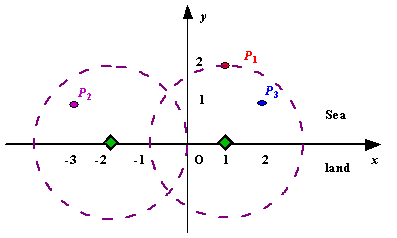
Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases. 

The input is terminated by a line containing pair of zeros 

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

Case 1: 2
Case 2: 1

---

 

鄙人仍然码力不够……建模虽然很快就建出来了，但是写了老半天交了近十发才磕磕碰碰A掉此题。

先来分析一下吧

题意

有n个在一二象限上的整点，要求在x轴上选取ans个点，满足以每个点为圆的图形并集包含n个整点且ans最小。

分析

因为这里每个监测站的有效范围为圆形，我们可以反过来以n个整点为圆心，d为半径作圆。每个圆在x轴上有两个交点，即映射后的线段，那么在这条线段上至少要有一个监测站。想到这里我马上就想起以前做过的一道叫做“监测站”的题目，于是很快开写了。

CE第一发

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<cmath>
 5 #include<algorithm>
 6 using namespace std;
 7 struct seg{int l,r;}f[1003];
 8 bool cmp(seg a, seg b){return a.r<b.r;}
 9 int n,d,ans;
10 inline void mapping(int x, int y, int i)
11 {
12     int ss = (int)sqrt(d*d-y*y);
13     f[i].l = x-ss;
14     f[i].r = x+ss;
15     return;
16 }
17 inline void work()
18 {
19     memset(f, 0, sizeof(f));
20     ans = -1;
21     for (int i=1; i<=n; i++)
22     {
23         int x,y;
24         scanf("%d%d",&x,&y);
25         if (y > d)return;
26         mapping(x, y, i);
27     }
28     ans = 0;
29     sort(f+1, f+n+1, cmp);
30     int i = 1;int j = 1;
31     while (j<=n)
32     {
33         ans++;
34         while(f[j].l<=f[i].r&&j<=n)j++;
35         i = j;
36     } 
37     return;
38 }
39 int main()
40 {
41     scanf("%d%d",&n,&d);
42     while (n!=0&&d!=0)
43     {
44         work();
45         printf("%d\n",ans);
46         scanf("%d%d",&n,&d);
47     }
48     return 0;
49 }

View Code

然后，愉快快快快快快快地CE了：）

woc在poj上面sqrt(int)会爆我的天哪。

解决方法：

　　1.$sqrt(int * 1.0)$

　　2.$sqrt((double) int)$

　　3.$sqrtf(int)$

WA第一发

　　隐隐发觉：似乎监测点可以不在整点上？把segment的l,r改成double

　　然而不只有这个错

WA第二发

　　手算一组数据发现线段要按左端点排序

　　然而不只有这个错

WA第三发

　　逐条check时候更新不对

　　第三发的

WA第四发

　　第四发交的

　　好的吧显而易见第四发也是错的

WA第五发

　　已经心态爆炸

　　找了一组讨论区里的数据跑了跑，发现！

　　我在判不可能情况时候就在子过程里return了

　　但这是多组数据啊！没读完的被当成下组数据读进去了……

　　还有，我一直把输出里的"Case"当成看看的……（毕竟有些USACO的题不就这样么）

　　没想到它居然是要输出的：）

AC这一发

　　

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<cmath>
 5 #include<algorithm>
 6 using namespace std;
 7 struct seg{double l,r;}f[1003];//WA-1
 8 bool cmp(seg a, seg b){return a.l-b.l<1E-5;}//WA-2
 9 int n,d,ans;
10 inline void mapping(int x,int y, int i)
11 {
12     double ss = sqrt(d*d*1.0-y*y*1.0);
13     f[i].l = x*1.0-ss;
14     f[i].r = x*1.0+ss;
15     return;
16 }
17 inline void work()
18 {
19     memset(f, 0, sizeof(f));
20     ans = -1;
21     bool fl = 0;
22     for (int i=1; i<=n; i++)
23     {
24         int x,y;
25         scanf("%d%d",&x,&y);
26         if (y > d)fl = 1;
27         mapping(x, y, i);
28     }if (fl)return;
29     ans = 0;
30     sort(f+1, f+n+1, cmp);
31     int i = 1;int j = 1;
32     while (j<=n)
33     {
34         ans++;
35         while((f[j].l-f[i].r<=1E-5)&&j<=n)
36         {
37             j++;
38             if (f[j].r-f[i].r < 1E-5)i = j;　　　　//WA-3 WA-4
39         }
40         i = j;
41     } 
42     return;
43 }
44 int main()
45 {
46     scanf("%d%d",&n,&d);
47     int t = 0;
48     while (n!=0||d!=0)
49     {
50         t++;
51         work();
52         printf("Case %d: %d\n",t,ans);　　//WA-5
53         scanf("%d%d",&n,&d);
54     }
55     return 0;
56 }

 

　　代码能力差还得多写题啊~

 

转载于:https://www.cnblogs.com/antiquality/p/8508539.html