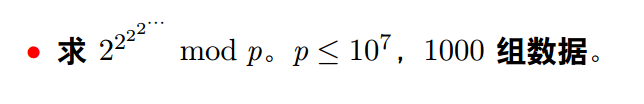
Luogu P4139 上帝与集合的正确用法【扩展欧拉定理】By cellur925-优快云博客

本文探讨了扩展欧拉定理的应用，并通过一个具体题目解析了如何使用递归和快速乘法来解决模幂运算问题。文章提供了详细的代码实现，包括phi函数初始化、快速乘法和快速幂函数，以及主函数中对多项式模数的处理。

题目中的式子很符合扩展欧拉定理的样子。（如果你还不知扩展欧拉定理，戳）。对于那一堆糟心的2，我们只需要递归即可，递归边界是模数为1.

另外，本题中好像必须要用快速乘的样子...否则无法通过...。

$Code$

 1 #include<cstdio>
 2 #include<algorithm>
 3  
 4 using namespace std;
 5 const int lim=10000010;
 6  
 7 int T,p;
 8 int phi[lim];
 9  
10 void init_phi()
11 {
12     phi[1]=1;
13     for(int i=2;i<=lim;i++) phi[i]=i;
14     for(int i=2;i<=lim;i++)
15         if(phi[i]==i)
16             for(int j=i;j<=lim;j+=i)
17                 phi[j]=phi[j]/i*(i-1);
18 }
19  
20 int mul(int a,int b,int mo)
21 {
22     int ans=0;
23     while(b)
24     {
25         if(b&1) ans=(ans%mo+a%mo)%mo;
26         b>>=1;
27         a=a%mo*2%mo;
28     }
29     return ans;
30 }
31  
32 int ksm(int a,int b,int mo)
33 {
34     int ans=1;
35     while(b)
36     {
37         if(b&1) ans=mul(ans,a,mo)%mo;
38         b>>=1;
39         a=mul(a,a,mo)%mo;
40     }
41     return ans;
42 }
43  
44 int work(int mod)
45 {
46     if(mod==1) return 0;
47     return ksm(2,work(phi[mod])+phi[mod],mod);
48 }
49  
50 int main()
51 {
52     init_phi();
53     scanf("%d",&T);
54     while(T--)
55     {
56         scanf("%d",&p);
57         printf("%d\n",work(p));
58     }
59     return 0;
60 }