软件工程第三次作业

软件工程第三次作业

问题描述

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

问题分析

完成此次作业我做了一下几点工作：

1. 编写最大字段和代码

2. 设计判断条件测试覆盖的测试用例

3. 使用junit进行单元测试

4. 使用随机数组改进测试，测试在线法和暴力法的效率差别

算法流程

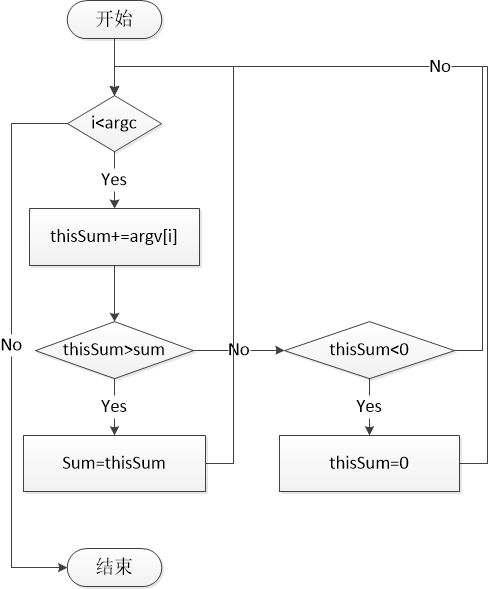
根据流程图设计了一组满足 覆盖的测试数据{2,1,-3}，语言功底有限，遂制作一张gif来演示一下这组数据的走向

我的尝试

分析一下这个在线法确实比暴力求解要好很多，那就用测试数据来说明一下。开始打算手写几十个数据上去，可惜时间还是0.000s。既然这样，就用随机数生产了1024个数据测了一下，时间上确实差了很多，算法的力量真是强大啊

0.095：0.000，效果很明显了。具体代码就放在coding了。
https://git.coding.net/liu1996/AssignmentThird.git

转载于:https://www.cnblogs.com/liuzhixin-123/p/8678946.html