冒泡与快速排序解析-优快云博客

很多人学习编程的时候，第一个接触到排序算法就是冒泡算法，它是最简单的交换类排序算法。此外，另一个著名的算法——快速排序算法，也属于交换类排序算法。

1 冒泡排序

(1) 基本思想
在非有序的序列中，两两比较相邻的元素，并交换不满足排序要求的元素对，直到整个序列都满足排序要求。由于每一趟排序，都会把非有序序列的最大元素（这里以升序为例）移动到非有序序列的末端，非常类似于水中气泡的上升过程，因此形象地称该算法为冒泡排序。

(2) 图文分析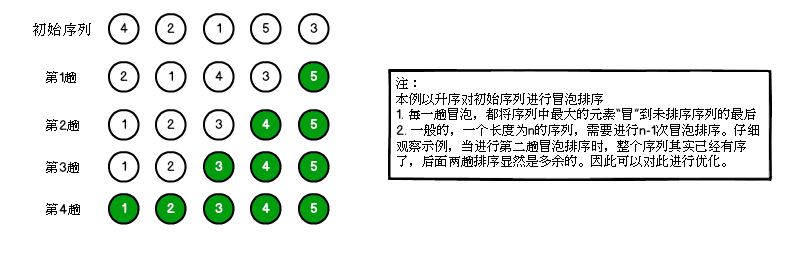

(3) 代码实现

// 冒泡排序
template <typename T>
void BubbleSort(T array[], int len)
{
    if(array == nullptr || len <= 0)
        return;
    int i, j;
    bool isSwap = true;    // 一趟比较中，标志是否有元素交换
    for(i = 0; i < len - 1 && isSwap; ++i)
    {
        isSwap = false;
        for(j = 1; j < len - i; ++j)
        {
            if(array[j] < array[j - 1])
            {
                isSwap = true;
                T temp = array[j];
                array[j] = array[j-1];
                array[j-1] = temp;
            }
        }
    }
}

(4) 测试

int main()
{
    int array[] = {4, 2, 1, 5, 3};
    int len = sizeof(array)/sizeof(int);
    BubbleSort(array, len);
    
    for(int i = 0; i<len; ++i)
        cout << array[i] << " ";
    cout<<endl;
    return 0;
}

测试结果

1 2 3 4 5

(5) 复杂度分析

a. 主要操作是比较相邻的两个元素

b. 最好的情况：初始序列为正序，一趟扫描之后便可完成排序，比较n-1次，交换0次，时间复杂度为O(n);

c. 最坏的情况：初始序列为逆序，需要进行n-1趟排序，比较和交换元素的次数达到最大，时间复杂度为O(n^2);

d. 平均时间复杂度为O(n);

e. 采用就地排序，空间复杂度为O(1)。

(6) 稳定性
冒泡排序比较的是相邻的两个元素比较，交换也发生在这两个元素之间。相同元素的相对位置没有发生改变，因此该算法是稳定的。

2 快速排序

(1) 基本思想

a. 找出一个元素（理论上可以随便找一个）作为基准(pivot),然后对数组进行分区操作,使基准左边元素的值都不大于基准值,基准右边的元素值都不小于基准值，如此作为基准的元素调整到排序后的正确位置。

b. 左、右子区间递归快速排序，将其他n-1个元素也调整到排序后的正确位置。

c. 最后每个元素都是在排序后的正确位置，排序完成。

(2) 图文分析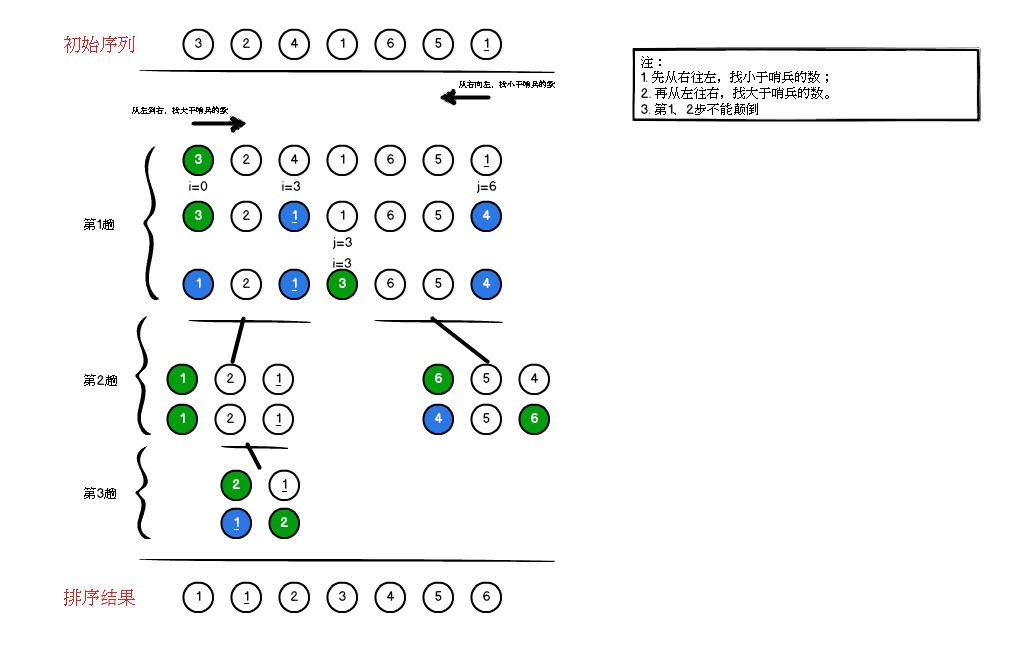

(3) 代码实现

// 快速排序
template <typename T>
void QuickSort(T array[], int left, int right)
{
    if(array == nullptr || left >= right)
        return;
    
    int i, j;
    i = left;
    j = right;
    T sentinel = array[left];       // sentinel作为基准数(哨兵)
    
    while(i < j)
    {
        while(array[j] >= sentinel && i < j)
            --j;
        while(array[i] <= sentinel && i < j)
            ++i;
        if(i < j)
        {
            T temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
    
    array[left] = array[i];
    array[i] = sentinel;
    
    QuickSort(array, left, i-1);
    QuickSort(array, i+1, right);
}

(4) 测试

int main()
{
    int array[] = {3,2,4,1,6,5,1};
    int len = sizeof(array)/sizeof(int);
    QuickSort(array, 0, len-1);
    
    for(int i = 0; i<len; ++i)
        cout << array[i] << " ";
    cout<<endl;
    return 0;
}

测试结果