Codeforces Round #370 (Div. 2) E. Memory and Casinos 线段树

E. Memory and Casinos

题目连接：

http://codeforces.com/contest/712/problem/E

Description

There are n casinos lined in a row. If Memory plays at casino i, he has probability pi to win and move to the casino on the right (i + 1) or exit the row (if i = n), and a probability 1 - pi to lose and move to the casino on the left (i - 1) or also exit the row (if i = 1).

We say that Memory dominates on the interval i... j if he completes a walk such that,

He starts on casino i.
He never looses in casino i.
He finishes his walk by winning in casino j. 

Note that Memory can still walk left of the 1-st casino and right of the casino n and that always finishes the process.

Now Memory has some requests, in one of the following forms:

1 i a b: Set .
2 l r: Print the probability that Memory will dominate on the interval l... r, i.e. compute the probability that Memory will first leave the segment l... r after winning at casino r, if she starts in casino l. 

It is guaranteed that at any moment of time p is a non-decreasing sequence, i.e. pi ≤ pi + 1 for all i from 1 to n - 1.

Please help Memory by answering all his requests!

Input

The first line of the input contains two integers n and q(1 ≤ n, q ≤ 100 000), — number of casinos and number of requests respectively.

The next n lines each contain integers ai and bi (1 ≤ ai < bi ≤ 109) — is the probability pi of winning in casino i.

The next q lines each contain queries of one of the types specified above (1 ≤ a < b ≤ 109, 1 ≤ i ≤ n, 1 ≤ l ≤ r ≤ n).

It's guaranteed that there will be at least one query of type 2, i.e. the output will be non-empty. Additionally, it is guaranteed that p forms a non-decreasing sequence at all times.

Output

Print a real number for every request of type 2 — the probability that boy will "dominate" on that interval. Your answer will be considered correct if its absolute error does not exceed 10 - 4.

Namely: let's assume that one of your answers is a, and the corresponding answer of the jury is b. The checker program will consider your answer correct if |a - b| ≤ 10 - 4.

Sample Input

3 13
1 3
1 2
2 3
2 1 1
2 1 2
2 1 3
2 2 2
2 2 3
2 3 3
1 2 2 3
2 1 1
2 1 2
2 1 3
2 2 2
2 2 3
2 3 3

Sample Output

0.3333333333
0.2000000000
0.1666666667
0.5000000000
0.4000000000
0.6666666667
0.3333333333
0.2500000000
0.2222222222
0.6666666667
0.5714285714
0.6666666667

Hint

题意

在第i个位置，你有pi的概率走到i+1，有(1-pi)的概率走到i-1

单点修改概率

区间查询从L开始，从R离开的概率是多少

题解：

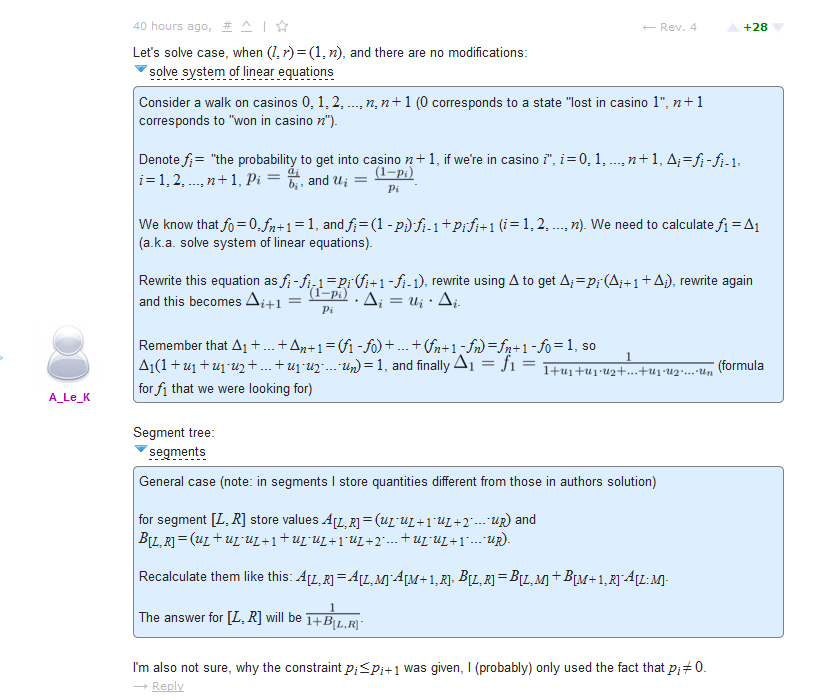
代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+7;
typedef pair<double,double> SgTreeDataType;
struct treenode
{
  int L , R  ;
  SgTreeDataType A;
  void updata(SgTreeDataType v)
  {
      A=v;
  }
};
pair<double,double>tmp=make_pair(1.0,0);
treenode tree[maxn*4];

inline void push_up(int o)
{
    tree[o].A.first = tree[o*2].A.first*tree[o*2+1].A.first;
    tree[o].A.second = tree[o*2].A.second + tree[o*2+1].A.second * tree[o*2].A.first;
}

inline void build_tree(int L , int R , int o)
{
    tree[o].L = L , tree[o].R = R;
    if (R > L)
    {
        int mid = (L+R) >> 1;
        build_tree(L,mid,o*2);
        build_tree(mid+1,R,o*2+1);
    }
}

inline void update(int QL,int QR,SgTreeDataType v,int o)
{
    int L = tree[o].L , R = tree[o].R;
    if (QL <= L && R <= QR) tree[o].updata(v);
    else
    {
        int mid = (L+R)>>1;
        if (QL <= mid) update(QL,QR,v,o*2);
        if (QR >  mid) update(QL,QR,v,o*2+1);
        push_up(o);
    }
}

inline SgTreeDataType query(int QL,int QR,int o)
{
    int L = tree[o].L , R = tree[o].R;
    if (QL <= L && R <= QR) return tree[o].A;
    else
    {
        int mid = (L+R)>>1;
        SgTreeDataType AA=tmp,BB=tmp,CC;
        if (QL <= mid) AA = query(QL,QR,2*o);
        if (QR > mid) BB = query(QL,QR,2*o+1);
        push_up(o);
        CC.first=AA.first*BB.first;
        CC.second=AA.second+BB.second*AA.first;
        return CC;
    }
}



int main()
{
    int n,q;
    scanf("%d%d",&n,&q);
    build_tree(1,n,1);
    for(int i=1;i<=n;i++)
    {
        double a,b;
        cin>>a>>b;
        double p = a/b;
        update(i,i,make_pair((1.0-p)/p,(1.0-p)/p),1);
    }
    for(int i=1;i<=q;i++)
    {
        int op,a,b,c;
        scanf("%d",&op);
        if(op==1)
        {
            scanf("%d%d%d",&a,&b,&c);
            double p = 1.0*b/(1.0*c);
            pair<double,double>D=make_pair((1-p)/p,(1-p)/p);
            update(a,a,D,1);
        }
        else
        {
            scanf("%d%d",&a,&b);
            double p = query(a,b,1).second;
            if(p<1e20)printf("%.12f\n",1.0/(1.0+p));
            else printf("0.000000000000\n");
        }
    }
    return 0;
}

转载于:https://www.cnblogs.com/qscqesze/p/5868047.html