南大算法设计与分析课程复习笔记(3)L3 - Recursion

一、递归方程

按照分治的思想，可以将一个递归的复杂度写成递归方程

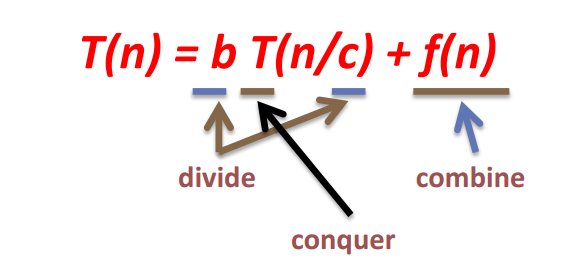
一、解递归方程--猜然后证明

该方法又称为代入法，步骤如下：

1、猜解的形式

2、数学归纳法证明正确

例子：

我们假设有如下递归式：

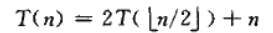
我们猜其解为T(n)=O(nlgn)，然后对递归式进行替换，得

 

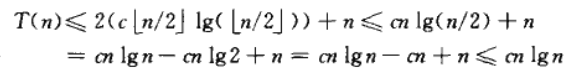
特别注意：我们替换之后得出的结果必须严格符合猜想，上面的例子如果最后得出T(n)<=cnlgn+1，都说明我们猜错了，需要选择新的猜解式。

二、解递归方程--递归树解

感觉这种方法比较的麻烦，一般用代入法和下面的master定理来做

例子

对于递归方程式：

它的递归树如下：

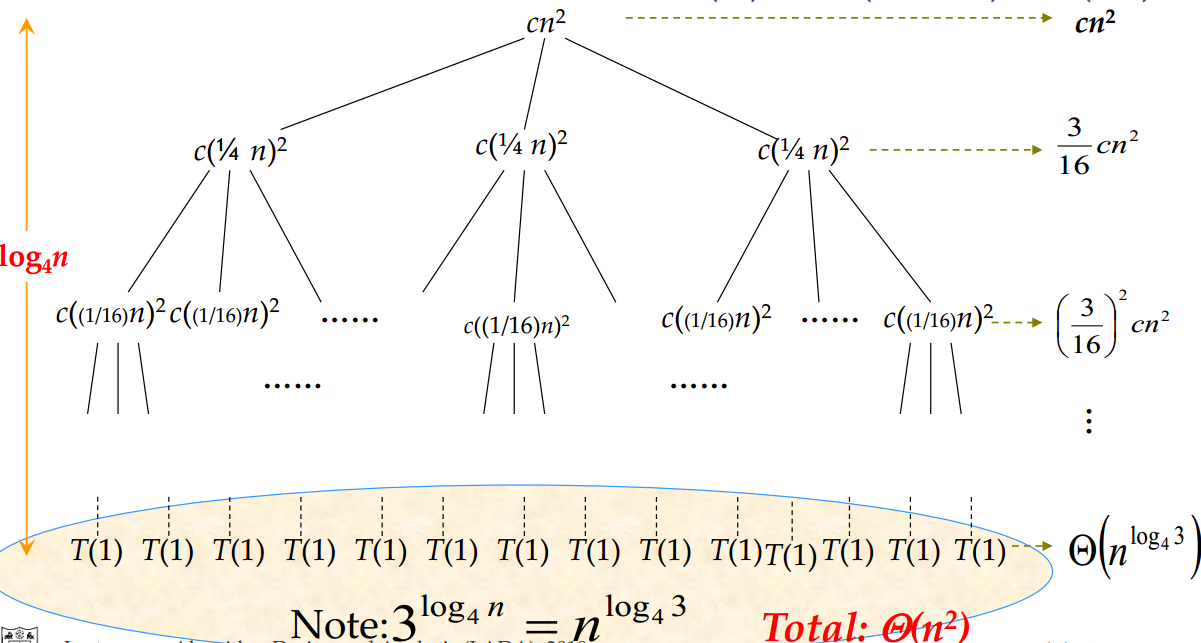
三、master定理

 如果a>=1和b>1，假设有一个递归函数，递归式如下：

 则有如下3条：

 

转载于:https://www.cnblogs.com/likaiming/p/8638593.html