Stability Analysis of Algorithms

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。对于同一个问题，使用不同的算法，也许最终得到的结果是一样的，比如排序就有前面的十大经典排序和几种奇葩排序，虽然结果相同，但在过程中消耗的资源和时间却会有很大的区别，比如快速排序与猴子排序。

算法稳定性分析。

一般研究算法性能会考虑复杂度问题居多，此外也会有算法的稳定性分析。

稳定性

根据个人研读论文后的浅薄观点归纳得到，【会一直更新】

对于一般的处理算法而言，稳定性主要由以下方面衡量：

1、当随着样本数量增加，或者试验次数的增加，算法的输出结果与精确解（期望解）相差不大，则可以说该算法是稳定的算法。

2、当输入信号不同时，算法如果都可以输出令人满意的解，则可以说该算法是稳定的。

3、如果可以证明该算法能够得到，并且始终得到全局最优解，可以说该算法是稳定的。

有时候稳定性也可以当作是鲁棒性理解。

排序算法

在网络上搜索算法稳定性分析，结果都是排序算法相关，在此也简单记录一下吧。

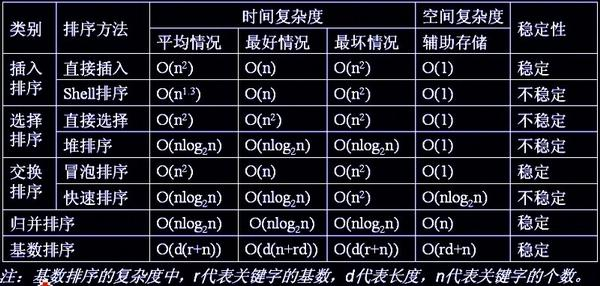
稳定性是针对数组中两个相等值的元素而言的。若两个相等元素排序前后相对位置没有改变，则说这个排序算法是稳定的。

常见算法的稳定性总结：

1. 插入排序：稳定。（在一个已经有序的小序列的基础上，一次插入一个元素。从有序序列的末尾开始比较，把待插入的元素和已经有序的最大者开始比起，比它大则直接插入在其后面。）
2. 冒泡排序：稳定。（每次只交换相邻的两个元素，把小的元素往前调，若两个元素相等将不会进行交换）
3. 归并排序：稳定。（采用分治法（Divide and Conquer）的典型应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。）
4. 基数排序：稳定。（基数排序就是，先按低位排序，逐次按高位排序，那么低位相同的数据元素其先后位置顺序即使在高位也相同时是不会改变的。）
5. 选择排序：不稳定。（给每个位置选择待排序元素中当前最小的元素。例：序列3 8 3 2 9，第一遍选择第1个元素3会和2交换，原序列中两个3的相对前后顺序就改变了）
6. 快速排序：不稳定。（快速排序有两个方向，左边的i下标一直往右走（当条件a[i] <= a[center_index]时））
7. 希尔排序：不稳定。（按照不同步长对元素进行插入排序）
8. 堆排序：不稳定。（一个长为n的序列，堆排序的过程是从第n/2开始和其子节点共3个值选择最大（大顶堆）或者最小（小顶堆）。当为n/2-1, n/2-2, ...1这些个父节点选择元素时，就会破坏稳定性。）

堆的结构是节点i的孩子为2*i和2*i+1节点，大顶堆要求父节点大于等于其2个子节点，小顶堆要求父节点小于等于其2个子节点。

算法复杂度

算法的时间复杂度通常用大O符号表述，定义为 **T[n] = O(f(n)) **。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。

如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。

上面公式中用到的 Landau符号是由德国数论学家保罗·巴赫曼（Paul Bachmann）在其1892年的著作《解析数论》首先引入，由另一位德国数论学家艾德蒙·朗道（Edmund Landau）推广。Landau符号的作用在于用简单的函数来描述复杂函数行为，给出一个上或下（确）界。在计算算法复杂度时一般只用到大O符号，Landau符号体系中的小o符号、Θ符号等等比较不常用。这里的O，最初是用大写希腊字母，但现在都用大写英语字母O；小o符号也是用小写英语字母o，Θ符号则维持大写希腊字母Θ。

一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度，可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分：

(1) 固定部分，这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。

(2) 可变空间，这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。

一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))，其中n为问题的规模，S(n)表示空间复杂度。

空间复杂度可以理解为除了原始序列大小的内存，在算法过程中用到的额外的存储空间。

当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；  
反之，求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。

另外，算法的所有性能之间都存在着或多或少的相互影响。因此，当设计一个算法(特别是大型算法)时，要综合考虑算法的各项性能，算法的使用频率，算法处理的数据量的大小，算法描述语言的特性，算法运行的机器系统环境等各方面因素，才能够设计出比较好的算法。

参见：https://mp.weixin.qq.com/s/W9Mz73A-Yqcsi6b2SBZwvQ

转载于:https://www.cnblogs.com/ytxwzqin/p/9859838.html