SVM理论之最优超平面

最优超平面(分类面)

 

 

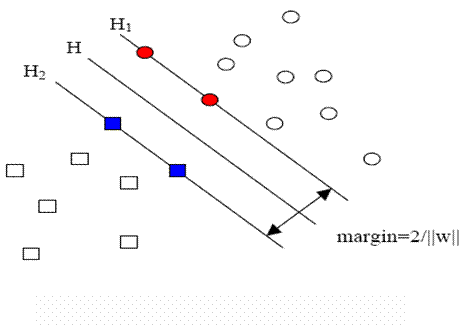
　　如图所示, 方形点和圆形点代表两类样本, H 为分类线,H1, H2分别为过各类中离分类线最近的样本且平行于分类线的直线, H1、H2上的点（xi, yi）称为支持向量， 它们之间的距离叫做分类间隔(margin)。中间那条分界线并不是唯一的，我们可以把它稍微旋转一下，只要不分错。所谓最优分类面(Optimal Hyper Plane)就是要求分类面不但能将两类正确分开(训练错误率为0),而且使分类间隔最大。推广到高维空间，最优分类线就变为最优分类面。支持向量是那些最靠近决策面的数据点，这样的数据点是最难分类的，因此,它们和决策面的最优位置直接相关。

　　我们有两个 margin 可以选，不过 functional margin 明显是不太适合用来最大化的一个量，因为在 hyper plane 固定以后，我们可以等比例地缩放 w 的长度和 b 的值，这样可以使得 f(x)=w^Tx+b 的值任意大，亦即 functional margin γ_f可以在 hyper plane 保持不变的情况下被取得任意大，而 geometrical margin γ_g则没有这个问题，因为除上了 ∥w∥ 这个分母，所以缩放 w 和b 的时候γ_g的值是不会改变的，它只随着 hyper plane 的变动而变动，因此，这是更加合适的一个 margin 。对一个数据点进行分类，当它的 margin 越大的时候，分类的 置信度(confidence) 越大。对于一个包含 n 个点的数据集，我们可以很自然地定义它的 margin 为所有这 n 个点的 margin 值中最小的那个γ_g=minγ_g，i，于是，为了使得分类的 confidence 高，我们希望所选择的 hyper plane 能够最大化这个 margin 值。简要地说，就是找到这样一个最优分类面，使离最优分类面最近的点的几何距离最大。即最优分类面的目标函数为：

   max γ_g  ,  s.t.  y_i(w^T ·x_i+b) = γ_g，i  >=  γ_g，i=1,…,n                                       &n