9.2.4 二次规划问题

9.2.4.1 基本数学原理

     如果某非线性规划的目标函数为自变量的二次函数，约束条件全是线性函数，就称这种规划为二次规划。其数学模型为：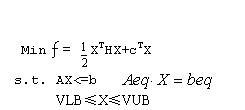

     其中，H, A,和Aeq为矩阵,f, b, beq, lb, ub,和x为向量。

9.2.4.2 相关函数介绍

     quadprog函数

     功能：求解二次规划问题。

     语法：

           x = quadprog(H,f,A,b)

           x = quadprog(H,f,A,b,Aeq,beq)

           x = quadprog(H,f,A,b,Aeq,beq,lb,ub)

           x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)

           x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

           [x,fval] = quadprog(...)

           [x,fval,exitflag] = quadprog(...)

           [x,fval,exitflag,output] = quadprog(...)

           [x,fval,exitflag,output,lambda] = quadprog(...)

    描述：

           x = quadprog(H,f,A,b) 返回向量x，最小化函数 1/2*x'*H*x + f'*x ，其约束条件为 A*x <= b。

           x = quadprog(H,f,A,b,Aeq,beq)仍然求解上面的问题，但添加了等式约束条件Aeq*x = beq。

           x = quadprog(H,f,A,b,lb,ub)定义设计变量的下界lb和上界ub，使得lb <= x <= ub。

           x = quadprog(H,f,A,b,lb,ub,x0)同上，并设置初值x0。

           x = quadprog(H,f,A,b,lb,ub,x0,options)根据options参数指定的优化参数进行最小化。

           [x,fval] = quadprog(...)返回解x处的目标函数值fval = 0.5*x'*H*x + f'*x。

           [x,fval,exitflag] = quadprog(...)返回exitflag参数，描述计算的退出条件。

           [x,fval,exitflag,output] = quadprog(...)返回包含优化信息的结构输出output。

           [x,fval,exitflag,output,lambda] = quadprog(...)返回解x处包含拉格朗日乘子的lambda参数。

    变量：

          各变量的意义同前。

    注意：

         1． 一般地，如果问题不是严格凸性的，用quadprog函数得到的可能是局部最优解。

         2． 如果用Aeq和Beq明确地指定等式约束，而不是用lb和ub指定，则可以得到更好的数值解。

         3． 若x的组分没有上限或下限，则quadprog函数希望将对应的组分设置为Inf（对于上限）或-Inf（对于下限），而不是强制性地给予上限一个很大的数或给予下限一个很小的负数。

         4． 对于大型优化问题，若没有提供初值x0，或x0不是严格可行，则quadprog函数会选择一个新的初始可行点。

         5． 若为等式约束，且quadprog函数发现负曲度(negative curvature)，则优化过程终止，exitflag的值等于-1。

   算法：

         大型优化算法  当优化问题只有上界和下界，而没有线性不等式或等式约束，则缺省算法为大型算法。或者，如果优化问题中只有线性等式，而没有上界和下界或线性不等式时，缺省算法也是大型算法。

         本法是基于内部映射牛顿法(interior-reflective Newton method)的子空间置信域法(subspace trust-region)。该法的具体算法请参见文献[2]。该法的每一次迭代都与用PCG法求解大型线性系统得到的近似解有关。

         中型优化算法   quadprog函数使用活动集法，它也是一种投影法，首先通过求解线性规划问题来获得初始可行解。

   诊断：

         1. 大型优化问题  大型优化问题不允许约束上限和下限相等，如若lb(2)==ub(2)，则给出以下出错信息：

            Equal upper and lower bounds not permitted in this large-scale method.Use equality constraints and the medium-scale method instead.

            若优化模型中只有等式约束，仍然可以使用大型算法；如果模型中既有等式约束又有边界约束，则必须使用中型方法。

       2．中型优化问题  当解不可行时，quadprog函数给出以下警告：

           Warning: The constraints are overly stringent;there is no feasible solution.

           这里，quadprog函数生成使约束矛盾最坏程度最小的结果。

           当等式约束不连续时，给出下面的警告信息：

           Warning: The equality constraints are overly stringent;there is no feasible solution.

           当Hessian矩阵为负半定时，生成无边界解，给出下面的警告信息：

           Warning: The solution is unbounded and at infinity;the constraints are not restrictive enough.

           这里，quadprog函数返回满足约束条件的x值。

局限性：

          1． 此时，显示水平只能选择'off'和'final'，迭代参数'iter'不可用。

          2．当问题不定或负定时，常常无解（此时exitflag参数给出一个负值，表示优化过程不收敛）。若正定解存在，则quadprog函数可能只给出局部极小值，因为问题可能时非凸的。

          3．对于大型问题，不能依靠线性等式，因为Aeq必须是行满秩的，即Aeq的行数必须不多于列数。若不满足要求，必须调用中型算法进行计算。

 

9.2.4.3 应用实例

[例一] 求解下面的最优化问题：

目标函数

约束条件

首先，目标函数可以写成下面的矩阵形式：

其中

输入下列系数矩阵：

H = [1 -1; -1 2]

f = [-2; -6]

A = [1 1; -1 2; 2 1]

b = [2; 2; 3]

lb = zeros(2,1)

然后调用二次规划函数quadratic：

[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb)

得问题的解

x =

     0.6667

     1.3333

fval =

    -8.2222

exitflag =

     1

output =

       iterations: 3

        algorithm: 'medium-scale: active-set'

    firstorderopt: []

     cgiterations: []

lambda.ineqlin

ans =

    3.1111

    0.4444

         0

lambda.lower

ans =

     0

     0

磁盘中本问题的M文件为opt24_1.m。

转载于:https://www.cnblogs.com/deeply/archive/2012/12/27/2835618.html