机器学习（二）--------单变量线性回归(Linear Regression with One Variable)

 

   面积与房价 训练集 （Training Set）

 Size       Price

2104       460

852         178

  。。。。。。

m代表训练集中实例的数量
x代表输入变量

y代表输出变量

（x，y）代表训练集中的实例

h代表方案或者假设        h =  a x + b

输入变量输入给h  得到输出结果  

因为只有一个特征   所以是单变量线性回归问题

a b就是代价参数    求ab就是建模    ab算完和实际的差距叫建模误差

寻找ab平方和最小点  就是代价函数  也叫平方误差函数

 这就是代价函数了   在两个参数下  真实值与求出的值的差的平方和  除以2m    其实就是求误差的平均数

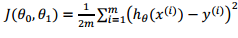
而最接近真实值的两个参数  就是使这个表达式最小

求出这两个参数

 

可以把两个参数作为坐标轴   表达式的值作为高度   画等高线图   便于理解    就是求高度最低点

 

而求参数所用到的方法叫做 梯度下降算法

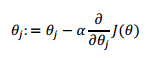
先初始化这个参数  然后每一次更新他   就是减去 α乘以J函数的导数   α叫做学习速率    随着越来越接近最小点   导数将接近为0    所以这个减去的值也将越来越小   直到找到最小点

 

由此得到了梯度下降的线性回归方程

 

用这个方程就是找到拟合面积房价的模型参数

 

 

转载于:https://www.cnblogs.com/tree1123/p/9990492.html