本文详细解析了ConcurrentHashMap的设计原理，包括其构造方法、put和remove操作、扩容算法等核心内容，阐述了如何解决多线程环境下的并发问题。
介绍:
ConcurrentHashMap 是从 JDK1.5 开始提供的并发容器, 为了解决多线程环境下 HashMap 的并发问题, 是线程安全的 HashMap.
一些参数介绍:
MAXIMUM_CAPACITY = 1 << 30: table 数组的最大大小
DEFAULT_CAPACITY = 16: table 数组默认大小
LOAD_FACTOR = 0.75f: 负载因子, 用于初始化和扩容, 固定,无法修改, 若构造方法传入 loadFactor 只有 table 初始化的时候有用到,后续是:
n = oldLength ; sizeCtl = (n << 1) - (n >>> 1); 也就是 sizeCtl = 1.5 * oldLength
TREEIFY_THRESHOLD = 8: 链表转化为树所需的节点数量
1.构造方法
首先从 ConcurrentHashMap 的初始化开始
ConcurrentHashMap 有几个构造方法,但都是对 sizeCtl 进行初始化,
1.8的 ConcurrentHashMap/HashMap 是在第一次 put 之后才进行table初始化 (initTable()) , 在第一次调用 initTable() 初始化数组之前, 这个sizeCtl 指的是数组大小, 在第一次初始化 table后, sizeCtl变为大小的 0.75倍(默认的负载因子 loadFactor) -> sizeCtl = n- (n >>>2) , 并且后面用来判断是否进行扩容.
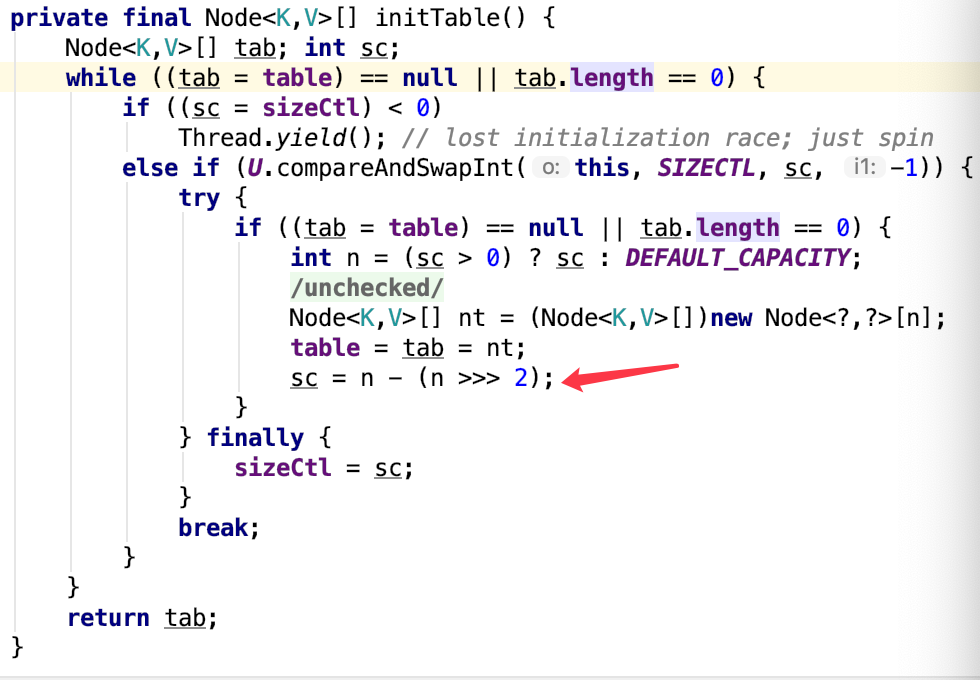
接下来是常用的一些方法
代码有点长,直接复制下来了
2.put方法:
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
// f 指的是头节点
Node<K,V> f; int n, i, fh;
// 初始化 tab[]
if (tab == null || (n = tab.length) == 0)
// 第一次，初始化节点数组
tab = initTable();
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
// (n - 1) & hash 获取该元素应该位于数组中的下标
// 查看数组中该下标的头节点是否唯为空, 为空的话,则用 CAS 尝试进行添加, 添加成功则返回, 失败则继续外层循环, 重新添加
if (casTabAt(tab, i, null,
new Node<K,V>(hash, key, value, null)))
break; // no lock when adding to empty bin
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
V oldVal = null;
// lock 头节点
synchronized (f) {
// 再次判断头节点是否为空, 防止在加锁前其他线程修改了头节点
if (tabAt(tab, i) == f) {
// 如果是链表节点
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f;; ++binCount) {
K ek;
// 如果找对应的节点，则替换旧值
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent)
e.val = value;
break;
}
// 保存当前节点
Node<K,V> pred = e;
// e 指向下一个节点
if ((e = e.next) == null) {
// 如果下一个节点 == null , 则 插入的节点为 pred(当前节点) 的下一个节点
pred.next = new Node<K,V>(hash, key,
value, null);
break;
}
}
}
// 当前是一棵树
else if (f instanceof TreeBin) {
Node<K,V> p;
binCount = 2;
//
if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
}
}
if (binCount != 0) {
// 如果链表长度 > 8 , 规定的最长链表长度，转化为 红黑树
if (binCount >= TREEIFY_THRESHOLD)
// 将链表转为红黑树
treeifyBin(tab, i);
// oldVal !=null ,表示已经插入成功,返回
if (oldVal != null)
return oldVal;
break;
}
}
}
// 如果是链表,binCount为该节点在链表中的位置(头节点的位置为1).如果是树, binCount = 2.
addCount(1L, binCount);
return null;
}
3.remove方法:
根据 key 查找到 node 的地方和上面的 put 方法是一样的, 区别就是查找到 node 后的操作.
// 链表节点
if (fh >= 0) {
validated = true;
for (Node<K,V> e = f, pred = null; ; ) {
K ek;
// 根据key,判断当前节点 e 是否是要查找的节点
if (e.hash==hash && ((ek = e.key)==key || (ek!=null && key.equals(ek)))) {
V ev = e.val;
// newVal == null 或者 newVal == oldVal 或者 equal
if (cv==null || cv==ev || (ev!=null && cv.equals(ev))) {
oldVal = ev;
if (value!=null)
e.val = value;
else if (pred!=null)
// 前一个节点指向下一个节点,即去掉当前节点
pred.next = e.next;
else
// 到这里表示 pred == null , 表示头节点,直接将下一个节点作为头节点
setTabAt(tab, i, e.next);
}
break;
}
// 保留前一个节点, e 指向下一个节点
pred = e;
if ((e = e.next)==null)
break;
}
} else if (f instanceof TreeBin) {
// 当前是一棵树,标记 validated
validated = true;
// 头节点是树节点
TreeBin<K,V> t = (TreeBin<K,V>) f;
// r = root , p -> 要删除的节点
TreeNode<K,V> r, p;
if ((r = t.root)!=null && (p = r.findTreeNode(hash, key, null))!=null) {
V pv = p.val;
if (cv==null || cv==pv || (pv!=null && cv.equals(pv))) {
oldVal = pv;
if (value!=null)
p.val = value;
else if (t.removeTreeNode(p))
// tree里删除p节点 ,返回true表示当前红黑树的节点数量较少,转化为链表
setTabAt(tab, i, untreeify(t.first));
}
}
}
4.扩容算法(同HashMap)
这个算法在的目的是返回一个不小于给定数字 c 的2的指数次方的大小
private static final int tableSizeFor(int c) {
int n = c - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
1.算法先 -1, 对应后面的 +1, 详细见3
2.经过四部逻辑或 && 无符号右移, 此时得到的数字 n = (x个0)111111, 此时后面全是1
3.最后一步, n+1 变成 n = (x-1个0)1000000, 正好是2的指数次幂的大小,如果之前是 1000000,已经是2的指数次幂大小 , n - 1 变成 0111111, 再+1,又变成了1000000, 不会变成 c 的 2倍
具体的图解：
四次逻辑或的目的是将最高位的1后面的数字都变为1, (x个0)(连续y个1)
假如n = 35 , 0010 0011
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1.第一步, n - 1 = 34 , 0010 0010
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
2.第二步, 第一次逻辑或 n |= n>>>1
0010 0011 | 0001 0001 = 0011 0011
此时n = 0011 0011 ,即 51
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
3.第三步,第二次逻辑或 n |=n>>>2
0011 0011 | 0000 1100 = 0011 1111
此时 n = 0011 1111, 即 63
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
4.第四步,第三次逻辑或 n |=n>>>4
此时上面第三步的结果 n = 63 --> 0011 1111, 最高位1后面的数字已经都是1，不用继续往下逻辑或了,如果是大点的数字，就需要进行后面的2次逻辑或
...省去5,6步,原因同上面第四步
7.计算最后的值
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
n的最大值不能超过规定的 MAXIMUM_CAPACITY (1<<30)
不超过规定的最大值的话，返回n + 1 , 所以上面的结果为 63 + 1 = 64
数字35返回的结果为64
即是,c = 35, 返回 64 , c = 119 返回 128 , c = 32 返回 32，如果本身已经是2的指数次幂大小， n-1之后，最高位1后面的逻辑位已经全是1，所以后面的逻辑或的操作都没有用，返回n+1,变回原数。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
