JZOJ 1714. 小x的三角形（triangles.pas/cpp）

1714. 【9.29NOIP普及模拟】小x的三角形（triangles.pas/cpp）
_{(File IO): input:triangles.in output:triangles.out}

时间限制: 1000 ms  空间限制: 128000 KB  具体限制 

Goto ProblemSet

题目描述

       小x和小o在一起研究各种图形的性质。小x发明了一个问题：一个完全无向图有n个顶点，选择m条边得到它们，并将剩余的   条边给小o。

       小x和小o喜欢图中的三角形，他们想知道他们得到的边所形成的图共形成了多少个三角形。

       图的顶点从1到n编号。

输入

       第一行包含两个用空格隔开的整数n和m，分别表示顶点数和小x选取的边数。

       接下来m行每行两个整数ai，bi，表示小x选取的第i条边连接顶点ai，bi，数据保证小x得到的图和初始的完全图无重       边和自环。

输出

输出一行一个整数，小x和小o得到的图所包含三角形的总数。

样例输入input1:

5 5

1 2

1 3

2 3

2 4

3 4





input2:


5 3

1 2

2 3

1 3

样例输出

output1:

3

output2:

4

数据范围限制

【数据范围】

对于20%的数据 1<=n<=20

对于60%的数据 1<=n<=100

对于100%的数据 1<=n<=20000, 0<=m<=10^6，m<=n(n-1)/2，1<=ai,bi<=n，ai≠bi

提示

【样例解释】

第一个样例，小x得到的图有两个三角形：(1,2,3)和(2,3,4)，小o有一个三角形(1,4,5)，所以总数是3。

第二个样例，小x的图只有一个三角形(1,2,3)，小o的图有3个三角形(1,4,5),(2,4,5)和(3,4,5)，所以总数是4。

 

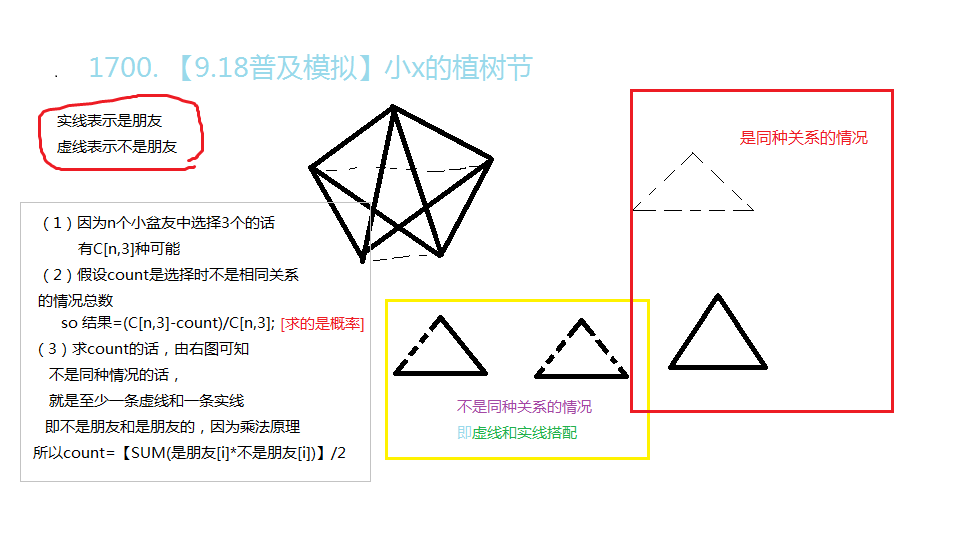
Idea from lyx & zyf ;

 借助几天前的一题来解释吧，我们可以把小x的边看做图中的实边，小o的边看做图中的虚边

他们两人所有的三角形就是同为虚边或者同为实边的种数之和， 具体求法如上：

P.S. 其实是CATALAN。。。。

 

 1 {
 2     by @bobble !
 3                     2017-1-19
 4 }
 5 program triangles;
 6 const
 7   inf='triangles.in';
 8   outf='triangles.out';
 9 var
10    s,e,i,n,m:longint;
11    ans,c,aaa:int64;
12    yes:array[0..20000] of longint;
13 begin
14   assign(input,inf);
15   assign(output,outf);
16   reset(input); rewrite(output);
17 
18   readln(n,m);
19   for i:= 1 to m do
20     begin
21          readln(s,e);
22          inc(yes[s]);
23        inc(yes[e]);
24     end;
25   for i:= 1 to n do 
26     c:=c+yes[i]*(n-yes[i]-1);
27   c:=c div 2;
28   aaa:=n*(n-1)*(n-2) div 6;
29   ans:=aaa-c;
30   writeln(ans);
31 
32   close(input);
33   close(output);
34 end.

 

转载于:https://www.cnblogs.com/bobble/p/6308628.html