本文总结了《程序设计与数据结构》第八周的学习内容，重点介绍了优先队列与堆的概念，包括最小堆和最大堆的特点，以及addElement、removeMin和findMin等基本操作的实现方法。同时，探讨了使用链表和数组实现堆的不同方式，以及堆排序的时间复杂度。
12.1 堆：
- 堆（heap） ： 具有两个附加属性 的二叉树；是一棵完全二叉树。
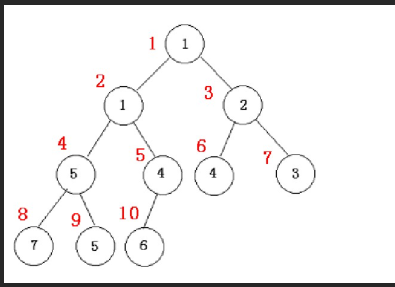
最小堆（minheap） ： 每一结点小于或等于其两个孩子；其根的两个孩子同样为最小堆。
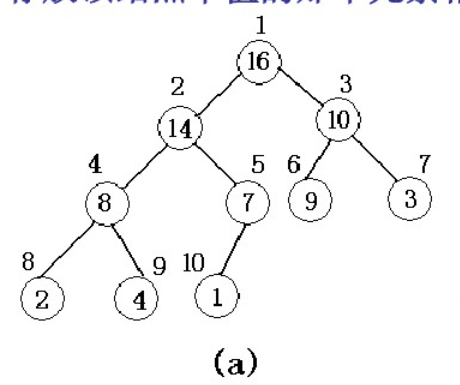
最大堆（maxheap） ： 每一结点大于或等于其两个孩子；其根的两个孩子同样为最大堆。
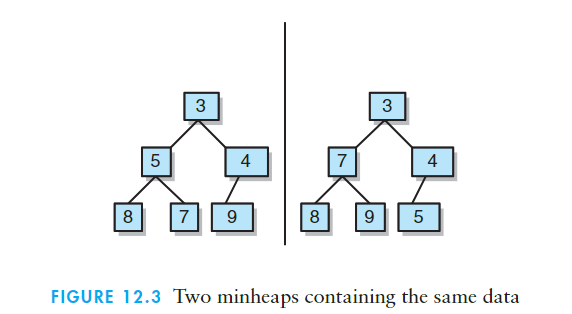
元素相同，构造的堆也可以不同：
- 堆的操作 ：
-
操作 说明 addElement 将给定元素添加到该堆中 removeMin 删除堆的最小元素 findMin 返回一个指向堆中最小元素的引用 - 12.1.1 addElement操作：
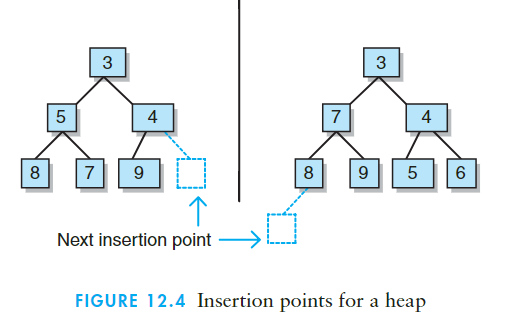
- 将给定的元素添加至适当位置，并维持好该堆的完全性和有序性
- 对于堆而言，因为其是一棵完全二叉树，所以在插入时会保持其完全性，所以对于新插入的结点来说，只存在一个正确的位置：要么其为h层左边的下一个空位置，要么其为h+1层左边的第一个位置。
- 12.1.2 removeMin操作：
- 删除堆的最小元素并返回；
- 用最末端的叶子替代根；
重构堆。
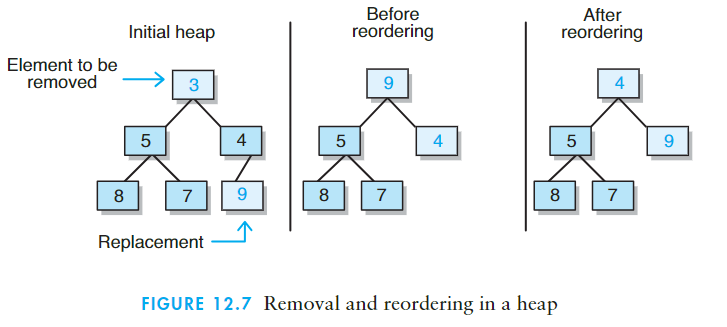
- 12.1.3 findMin操作：
堆的根处存储的是堆中的最小元素，因此只需返回其即可。
- 12.2 使用堆：优先级队列
优先级队列（priority queue） 和通常的栈和队列一样，但里面的每一个元素都有一个优先级 ，在处理的时候，首先处理优先级最高的。如果两个元素具有相同的优先级，则按照他们插入到队列中的先后顺序处理。
虽然堆并非一个队列，但其提供了一个高效 的优先级队列实现。
- 12.3 使用链表实现堆
为能向上遍历树，每个结点存储了指向双亲的指针。
- 12.3.1 addElement操作：
- 在恰当位置添加一个新元素
- 对堆进行重排序以维持其排序属性
- lastNode指针重新设定为指向最新的最末结点
时间复杂度O（log n）
12.3.2 removeMin操作：
- 用存储在最末结点处的元素替换存储在根处的元素
- 对堆进行重排序
- 返回初始根元素
- 时间复杂度O（log n）
12.3.3 findMin操作：
- 返回指向存储在堆根处元素的引用
时间复杂度为O（1）
12.4 使用数组实现堆
- 树根位于位置0处；
- 左孩子位于2n+1处
右孩子位于2（n+1）处
- 12.4.1 addElement操作：
- 在恰当位置添加一个新元素
- 对堆进行重排序以维持其排序属性
- count递增加1
时间复杂度O（log n）
12.4.2 removeMin操作：
- 用存储在最末结点处的元素替换存储在根处的元素
- 对堆进行重排序
- 返回初始根元素
- 时间复杂度O（log n）
12.4.3 findMin操作：
- 返回指向存储在堆根处元素的引用（该引用指向存储在堆的根处或数组位置0处的元素）
时间复杂度为O（1）
12.5 使用堆：堆排序
- 添加列表中的每个元素
一次删除一个元素
时间复杂度为O（n log n）
- 问题1：2-3-4树？
- 解决：
问题1：如何删除某一指定结点的子树。
解决：
- 错题1：上周无任何错题。
- 解决：
- 错题2：
- 解决：
- 错题3：
- 解决：
- 本周结对学习情况：
- 20172316赵乾宸
- 博客中值得学习的或存在问题：
- 20172329王文彬
- 博客中值得学习的或存在问题：
- 博客内容充实、排版整齐、对教材内容有经过一番认真思考、继续保持。
- 代码截图做标注时应尽量避免遮挡代码。
- Markdown的部分缩进有误。
- 教材问题2提出得很好，可以看出近断时间来反复使用链表、数组去实现同一类型的数据结构起得了一定的成效。
- 20172316赵乾宸
| 代码行数（新增/累积） | 博客量（新增/累积） | 学习时间（新增/累积） | |
|---|---|---|---|
| 目标 | 3000行 | 15篇 | 300小时 |
| 第一周 | 0/0 | 1/1 | 12/12 |
| 第二周 | 935/935 | 1/2 | 24/36 |
| 第三周 | 849/1784 | 1/3 | 34/70 |
| 第四周 | 3600/5384 | 1/5 | 50/120 |
| 第五周 | 2254/7638 | 1/7 | 50/170 |
| 第六周 | 2809/10447 | 1/9 | 45/215 |
| 第七周 | 3700/14147 | 1/10 | 40/255 |
| 第八周 | 3422/17569 | 1/11 | 36/291 |
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
