数据的描述统计量

最新推荐文章于 2024-06-16 16:23:02 发布

转载最新推荐文章于 2024-06-16 16:23:02 发布 · 192 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/RHadoop-Hive/p/10167495.html

本文详细介绍如何使用R语言进行数据的统计分析，包括描述数据的水平、差异和分布形状的统计量计算方法。通过实例展示了平均数、分位数、极差、方差等统计指标的计算过程，并解释了偏度和峰度的概念。

一、本文简介　　

　　一组样本数据分布的数值特诊可以从三个方面进行描述：

1、数据的水平：也称为集中趋势或位置度量，反应全部数据的数值大小。

2、数据的差异：反应数据间的离散程度。

3、分布的形状：反应数据分布的偏度和峰度。

本文基于R实现描述数据的各统计量的计算方法。

二、描述水平的统计量

> head(iris[,-5],20)
   Sepal.Length Sepal.Width Petal.Length Petal.Width
1           5.1         3.5          1.4         0.2
2           4.9         3.0          1.4         0.2
3           4.7         3.2          1.3         0.2
4           4.6         3.1          1.5         0.2
5           5.0         3.6          1.4         0.2
6           5.4         3.9          1.7         0.4
7           4.6         3.4          1.4         0.3
8           5.0         3.4          1.5         0.2
9           4.4         2.9          1.4         0.2
10          4.9         3.1          1.5         0.1
11          5.4         3.7          1.5         0.2
12          4.8         3.4          1.6         0.2
13          4.8         3.0          1.4         0.1
14          4.3         3.0          1.1         0.1
15          5.8         4.0          1.2         0.2
16          5.7         4.4          1.5         0.4
17          5.4         3.9          1.3         0.4
18          5.1         3.5          1.4         0.3
19          5.7         3.8          1.7         0.3
20          5.1         3.8          1.5         0.3

2.1、平均数

> mean(iris$Sepal.Length)
[1] 5.843333

2.2、分位数

1、中位数

> median(iris$Sepal.Length)
[1] 5.8

2、四分位数

> quantile(iris$Sepal.Length,probs = c(0.25,0.75),type = 6)
25% 75% 
5.1 6.4

3、百分位数

> quantile(iris$Sepal.Length,probs = c(0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9),type = 6)
 10%  20%  30%  40%  50%  60%  70%  80%  90% 
4.80 5.00 5.23 5.60 5.80 6.10 6.30 6.58 6.90

2.3、众数

> which.max(table(iris$Sepal.Length))
5 
8

三、描述差异的统计量

3.1、极差和四分位数

1、极差

> range<-max(iris$Sepal.Length)-min(iris$Sepal.Length)
> range
[1] 3.6

2、四分位差

> IQR(iris$Sepal.Length,type = 6)
[1] 1.3

3.2、方差和标准差

> var(iris$Sepal.Length)
[1] 0.6856935
> sd(iris$Sepal.Length)
[1] 0.8280661

3.3、变异系数

> mean<-apply(iris[,1:4],1,mean)
> sd<-apply(iris[,1:4],1,sd)
> cv<-sd/mean
> x<-data.frame("平均数"=mean,"标准差"=sd,"变异系数"=cv)
> round(x,4)
    平均数 标准差 变异系数
1    2.550 2.1794   0.8547
2    2.375 2.0370   0.8577
3    2.350 1.9975   0.8500
4    2.350 1.9122   0.8137
5    2.550 2.1564   0.8456
6    2.850 2.2308   0.7828
7    2.425 1.9363   0.7985
8    2.525 2.1093   0.8354
9    2.225 1.8228   0.8192
10   2.400 2.0688   0.8620
11   2.700 2.3080   0.8548
12   2.500 2.0166   0.8066
13   2.325 2.0320   0.8740
14   2.125 1.8839   0.8866
15   2.800 2.5665   0.9166
16   3.000 2.4671   0.8224
17   2.750 2.3072   0.8390
18   2.575 2.1438   0.8325
19   2.875 2.3698   0.8243
20   2.675 2.1731   0.8124

> boxplot(iris[,1:4],notch = TRUE,col = "lightblue",ylab="花瓣长度",xlab="长度")

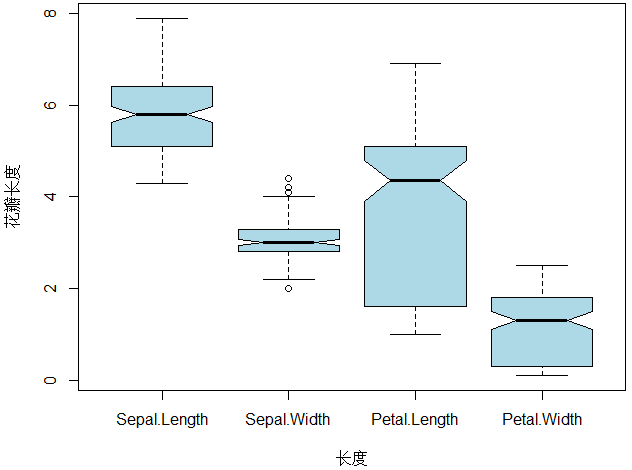
3.4、标准分数

> as.vector(round(scale(iris[,1:4]),4))
  [1] -0.8977 -1.1392 -1.3807 -1.5015 -1.0184 -0.5354 -1.5015
  [8] -1.0184 -1.7430 -1.1392 -0.5354 -1.2600 -1.2600 -1.8638
 [15] -0.0523 -0.1731 -0.5354 -0.8977 -0.1731 -0.8977 -0.5354
 [22] -0.8977 -1.5015 -0.8977 -1.2600 -1.0184 -1.0184 -0.7769
 [29] -0.7769 -1.3807 -1.2600 -0.5354 -0.7769 -0.4146 -1.1392
 [36] -1.0184 -0.4146 -1.1392 -1.7430 -0.8977 -1.0184 -1.6223
 [43] -1.7430 -1.0184 -0.8977 -1.2600 -0.8977 -1.5015 -0.6561
 [50] -1.0184  1.3968  0.6722  1.2761 -0.4146  0.7930 -0.1731
 [57]  0.5515 -1.1392  0.9138 -0.7769 -1.0184  0.0684  0.1892
 [64]  0.3100 -0.2939  1.0345 -0.2939 -0.0523  0.4307 -0.2939
 [71]  0.0684  0.3100  0.5515  0.3100  0.6722  0.9138  1.1553
 [78]  1.0345  0.1892 -0.1731 -0.4146 -0.4146 -0.0523  0.1892
 [85] -0.5354  0.1892  1.0345  0.5515 -0.2939 -0.4146 -0.4146
 [92]  0.3100 -0.0523 -1.0184 -0.2939 -0.1731 -0.1731  0.4307
 [99] -0.8977 -0.1731  0.5515 -0.0523  1.5176  0.5515  0.7930
[106]  2.1214 -1.1392  1.7591  1.0345  1.6384  0.7930  0.6722
[113]  1.1553 -0.1731 -0.0523  0.6722  0.7930  2.2422  2.2422
[120]  0.1892  1.2761 -0.2939  2.2422  0.5515  1.0345  1.6384
[127]  0.4307  0.3100  0.6722  1.6384  1.8799  2.4837  0.6722
[134]  0.5515  0.3100  2.2422  0.5515  0.6722  0.1892  1.2761
[141]  1.0345  1.2761 -0.0523  1.1553  1.0345  1.0345  0.5515
[148]  0.7930  0.4307  0.0684  1.0156 -0.1315  0.3273  0.0979
[155]  1.2450  1.9333  0.7862  0.7862 -0.3610  0.0979  1.4745
[162]  0.7862 -0.1315 -0.1315  2.1627  3.0805  1.9333  1.0156
[169]  1.7039  1.7039  0.7862  1.4745  1.2450  0.5567  0.7862
[176] -0.1315  0.7862  1.0156  0.7862  0.3273  0.0979  0.7862
[183]  2.3922  2.6216  0.0979  0.3273  1.0156  1.2450 -0.1315

四、描述分布形状的统计量

4.1、偏度系数

> library(agricolae)
> skewness(iris$Sepal.Length)
[1] 0.314911

4.2、峰度系数

> kurtosis(iris$Sepal.Length)
[1] -0.552064

转载于:https://www.cnblogs.com/RHadoop-Hive/p/10167495.html