5.1-1:
Since we can compare between any two elements, we know the total order on the ranks of the candidates.
5.1-2:
RANDOM(a,b)
%range = b - a;
%d = the number of binary bits %range has
do
for(%i = 1 to %d):
%i th bit of integer %res = rand(0,1);
while(%res > %range);
return (a + %res);
Each time of while loop need O(log(b-a)) time, and the expectation of that while loop is constant. Therefore, it takes time O(log(b-a))
5.1-3:
UNBIASED-RANDOM()
do:
a = random(0,1);
b = random(0,1);
while(a==b);
return a;
The possibility for (1,0) is p(1-p), and the same for (0,1).
Thus, the possibility for the termination of while loop is 2p(1-p);
the expectation is 1/(2p(1-p))
Thus the expected running time is O(1/(2p(1-p)))
I've spent some time thinking about how to find this expectation:
Suppose the possibility for event e happen is p, then the exception is:
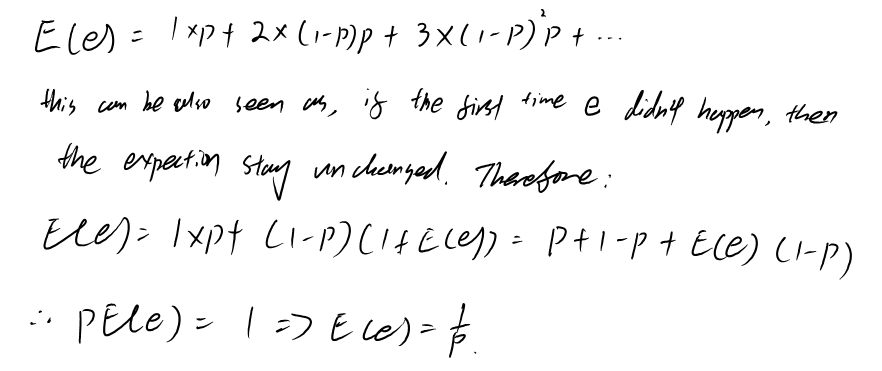







 本文详细探讨了两种随机数生成算法:一种用于在指定范围内生成随机整数,另一种用于生成无偏随机数。前者考虑了循环中每次所需的时间复杂度,并得出期望运行时间为O(log(b-a))的结论;后者分析了无偏随机数生成的期望运行时间,并计算其为O(1/(2p(1-p)))。
本文详细探讨了两种随机数生成算法:一种用于在指定范围内生成随机整数,另一种用于生成无偏随机数。前者考虑了循环中每次所需的时间复杂度,并得出期望运行时间为O(log(b-a))的结论;后者分析了无偏随机数生成的期望运行时间,并计算其为O(1/(2p(1-p)))。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








