简单链表

1. 对头结点进行更新操作时要用指针的指针。
2. 链表操作时候记得要追踪好头结点，遍历时要不断检测是否到达链表尾部。
3. 链表的插入和删除：

bool delete(Element* elem);(检查有0个元素；有1个元素；有2个元素是否能正确运行)

bool insertAfer(Element* elem, int data);

在删除操作时我们考虑3种情况：

• 删除头结点（更新头结点）
• 删除中间的一般节点
• 删除尾节点（更新尾节点，其实删除的情况和第二种差不多，只是要判断更新尾节点）

4. 栈的实现：

class Stack{

public:

Stack():head(null) {};

~Stack();

void push(void *data);

void *pop();

protected:

class Element{

public :

Element(Elemet *n, void *d): next(n), data*(d){}

Element *getNext() const { return next;}

Element *value() const {return data;}

private:

Element* next;

void* data;

}

Element* head;

};

 

Stack::~Stack(){

while(head){

Element *next = head->next;

delete head;

head = next;

}

}

void Stack::push(void *data){

Element *element = new Element(head, data);

head = element;

}

void Stack::pop(){

Element *popElement = head;

void *data;

if(head ==NULL) throw StackError(E_Empty);

data = head->value();

head = head->getNext();

delete popElement;

return data;

}

 

5. 对函数中bug的分析：

• 检查数据的传入是否正确
• 检查每一行是否能正确运行
• 数据的返回是否正确
• 边界条件等常见错误条件

6. 链表中倒数第m个元素

• 总共有n个元素，设l=n-m,那么指针走l-1步就到达第m个元素了。但此方法需要遍历链表两次，第一

次是遍历获取n的值，然后第二次找到所需位置的数。

• 设置两个指针，第一个指针先走m步，然后两个指针一起走，因为走得时候两个指针之间距离都是m

所以当第一个指针走到尾部时候，第二个指针刚好走到倒数第m个数。（此时应注意m<n的情况）

7. 链表的展平和恢复

题目是这样的：

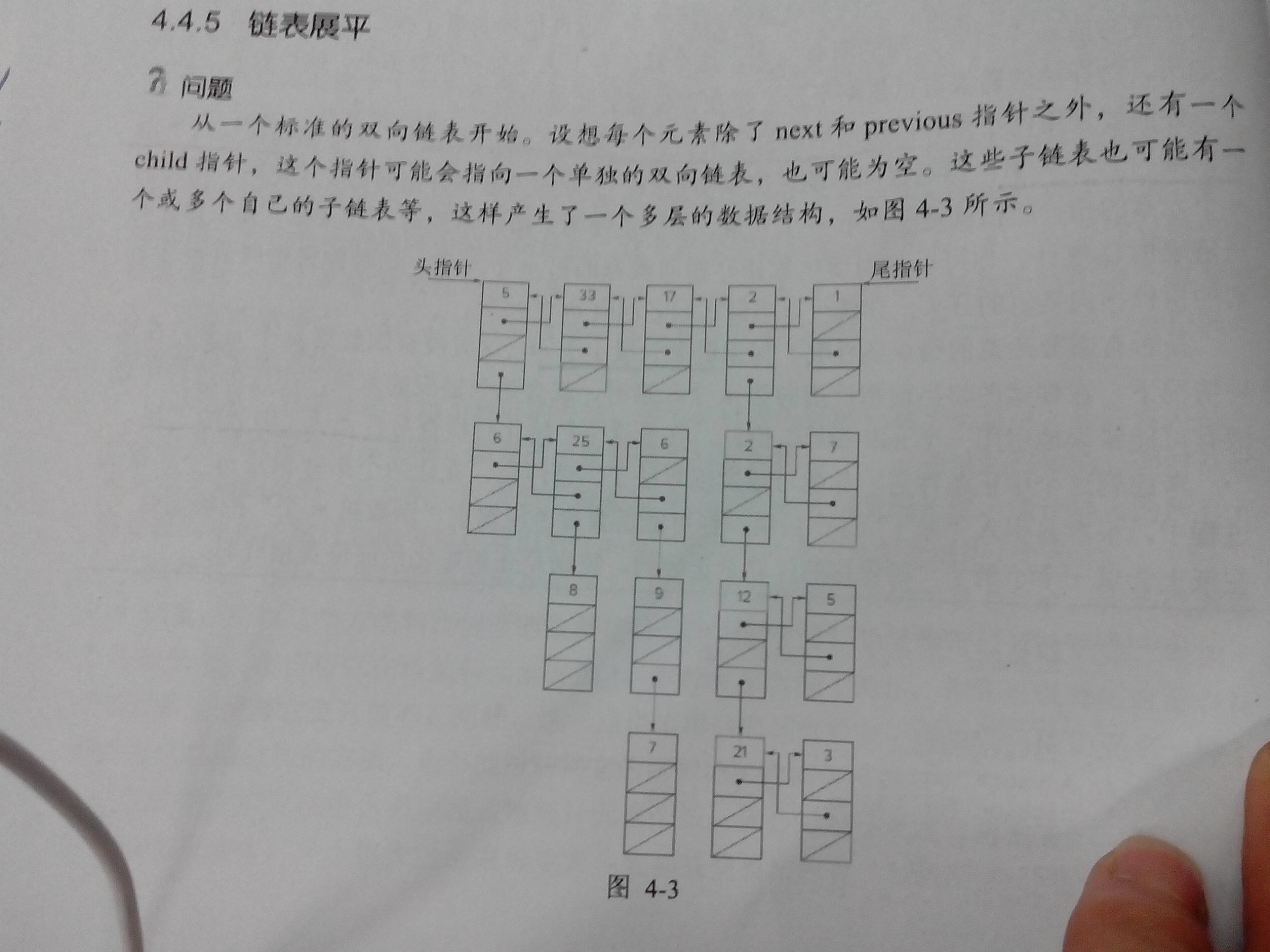
链表的展平：

此时解题思路应该和树的是差不多的，先找遍历顺序，然后找相应的算法来实现相应的遍历。书中选择的是层次遍历。图中第二层是有两个子链表组成的，先把第一个子链表附加到结尾，然后将第二个子链表附加到结尾。此时结尾应该是7这个节点，然后继续循环到第二层时就会把第三层的三个子链表附加到后面，以此类推，最后实现了链表的展平。

Start at the beginning of the first level

While you are not at the end of the level

If the current node has a child

Append the child to the end of the level

Update the tail pointer

Advance to next node;

链表的恢复：

书中是按照恢复到深度优先来做的。同样是考虑从第一行开始，当遇到有子节点时遍历他每个的子链表。此处应有递归：每次当你找到一个有子节点的节点时，将子节点从原链表中分离，然后遍历新的子节点，之后再继续遍历源节点。

Explore path:

While not at the end

If current node has a child

Separate the child from its previous node

Explore path beginning with the child

Go onto the next node

8. 判断链表是否是循环链表

• 把当前节点的next指针和之前的所有指针进行比较，看是否已经遍历过。O(n2)
• 设置两个指针，慢的指向头结点，快的指向头结点下个节点。快的每次走两步，慢的每次走一步，

当快的节点等于慢的节点或者走到慢的节点前面时候就说明是循环链表。

转载于:https://www.cnblogs.com/cnguoyu123/p/4472538.html