机器学习（四）--------逻辑回归(Logistic Regression)

 

 

 

逻辑回归(Logistic Regression)

线性回归用来预测，逻辑回归用来分类。

线性回归是拟合函数，逻辑回归是预测函数

 

逻辑回归就是分类、

分类问题用线性方程是不行的   线性方程拟合的是连续的值     

逻辑回归是分类问题   比如肿瘤问题    只有 0 ，1 两种情况

逻辑回归的方程写成     

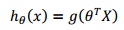
X是特征向量   theta是参数向量    theta转置乘以特征向量 就是参数与特征相乘

g代表逻辑函数     一个常用的s型逻辑函数就是 ：

 

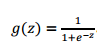
图为：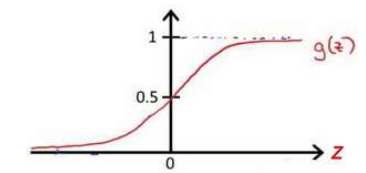

 

python代码为：

 

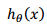的意义呢     因为结果是 0 1  所以他的意义其实是为1的概率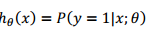

 

 

决策边界decision boundary

比如说模型是这样的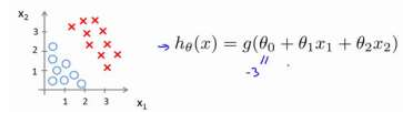

g还是和上边一样  0 1  逻辑回归都用这个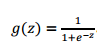

 

我需要做的就是用一条线把他们分开   这条线可能是直线  也可能是更复杂的线

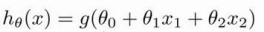
数? 是向量[-3 1 1]。 则当−3 + ?1 + ?2 ≥ 0，即?1 + ?2 ≥ 3时，模型将预测 ? =
1，那么这条线就是?1 + ?2 = 3

 

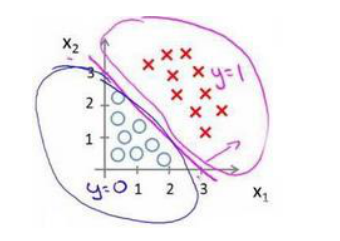
还有更复杂的场景：

 

 

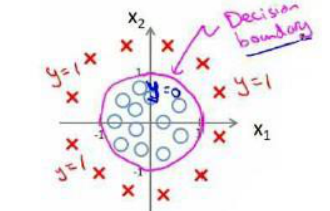
ℎ?

(?) = ?(?0 + ?1?1 + ?2?2 + ?3?1
2 + ?4?2
2
)是[-1 0 0 1 1]，则我们得到的判定边界恰好是圆
点在原点且半径为 1 的圆形

 

代价函数：的逻辑回归模型的拟合问题

 对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们
也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将ℎ?
(?) =
1
1+?
−??
?
带入到这样
定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）

 

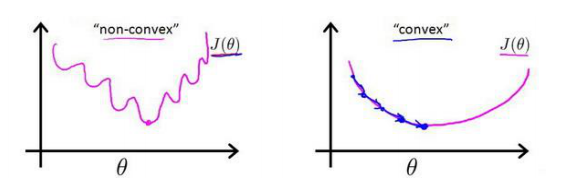
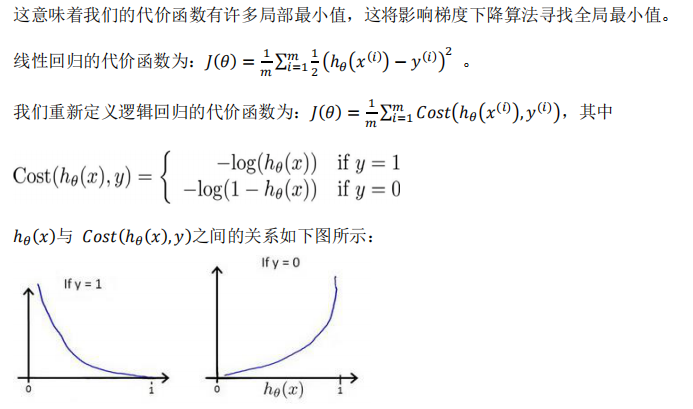
除了梯度下降，还有其他一些算法共轭梯度（Conjugate Gradient），局部优化法(Broydenfletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)。

也可能用特征缩放来进行优化。还有其他的一些优化方法。

 

 

多类别的分类问题

 

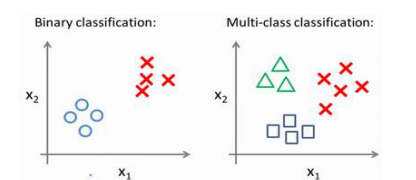
这种情况要定义正向类，负向类，进行多次决策。

 

转载于:https://www.cnblogs.com/tree1123/p/10113068.html