AC自动机

AC自动机

AC自动机比kmp要强，可以解决多模式匹配问题。

假设我们有n个模式串\(s_i\)，我们可以把它们放到Trie树T中，根据Trie来匹配哪个串被选择（到一个点表示这个点代表的字符被选择了）。但是，有可能遇到失配的情况，失配时该怎么办呢？

如图，假设现在模式串和原串匹配到abcd，原串的下一个是e，而Trie树当前结点的子结点中没有e。那么，由于cd出现在模式串中，应向cde中的d连边，表示原来的点匹配失败时到这个点去继续尝试匹配。这种边称作fail边。由此有个显而易见的规律：当前点向代表某模式串前缀的点A连边，并且A代表原路径中尽可能长的后缀。（对应在例子里就是cd是abcd的后缀，且是某个模式串的前缀，因此两个d之间连边）。

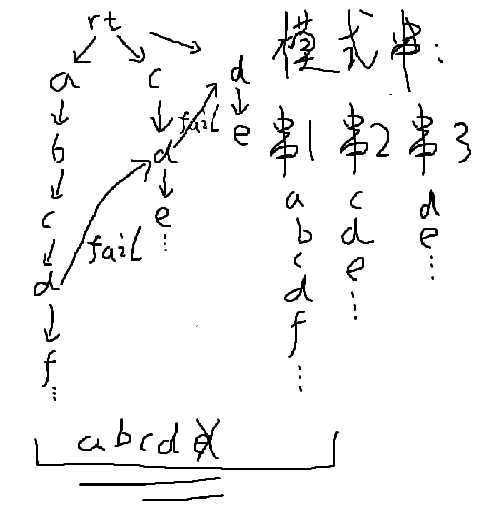
由于在遇到孩子是空结点的情况时，我们只会去fail边，因此可以直接把这个孩子设成fail边所指向的结点，更加方便。因为fail边只会往回连（串的后缀长度不大于串），我们可以采用bfs的方式求出每个点的fail指针（根的fail指针指向自己，孩子x的fail指针就是当前点的fail指向的孩子x）。构造出的Trie树+fail边的东西，我们就叫他AC自动机。

有了AC自动机，匹配原串就很容易了。例如当前要求的是每个模式串出现的次数，那么匹配到当前字符时，沿着当前点的fail边一直迭代下去，每一个有权值的点都代表一个模式串，统计它们即可（形象理解，就是在原串中当前处理位置的前面一段已匹配字符串不断缩小，其中某些是模式串）。注意一个结点的权值可以有很多种定义方式，本题中表示与它对应的模式串个数。

如果问题更加简单，变成求所有模式串出现的次数，那甚至连fail边都不用考虑了，直接把这个点通过fail边连向的点的权值加到这个点来即可。此时这个点的权值可以理解为当前模式串的后缀中，模式串的个数。这样做非常方便，在AC自动机上DP中很常见。

下面是洛谷P3808模板题的代码。

// luogu-judger-enable-o2
#include <cstdio>
#include <cstring>
using namespace std;

const int maxnode=1e6+5, maxm=1e6+5;
int n, m, cnts, ans, fail[maxnode], son[maxnode][26], p[maxnode];
char a[maxnode], T[maxm];

void ins(char *a, int len){
    int now=0;
    for (int i=0; i<len; ++i){
        if (!son[now][a[i]-'a']) son[now][a[i]-'a']=++cnts;
        now=son[now][a[i]-'a']; }
    ++p[now];
}

int q[maxnode], hd, tl;
void build(){  //宽搜 
    hd=tl=0;
    for (int i=0; i<26; ++i)
        if (son[0][i]) q[tl++]=son[0][i];
    while (hd<tl){
        int now=q[hd++]; 
        for (int i=0; i<26; ++i)
            if (son[now][i]){  //有孩子时的fail只是为了方便求出无孩子时的fail 
                fail[son[now][i]]=son[fail[now]][i], q[tl++]=son[now][i]; 
                //p[son[now][i]]+=p[fail[son[now][i]]];  //如果求的是总的出现次数就可以这么写，后面直接统计即可 
            }  //如果now是根的话就会出现错误,因为now的父亲还是now 
            else son[now][i]=son[fail[now]][i];  //直接把孩子设成fail，这样就不需要fail了 
    }
}

int main(){
    while (~scanf("%d", &n)){
        memset(son, 0, sizeof(son)); memset(fail, 0, sizeof(fail));
        for (int i=1; i<=n; ++i){
            scanf("%s", a); ins(a, strlen(a)); }
        build(); int now=0; ans=0;
        scanf("%s", T); m=strlen(T);
        for (int i=0; i<m; ++i){
            now=son[now][T[i]-'a'];
            for (int t=now; t&&~p[t]; t=fail[t]) ans+=p[t], p[t]=-1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

转载于:https://www.cnblogs.com/MyNameIsPc/p/9307204.html