本文深入讲解数字信号处理的基础概念，包括信号与曲线的数字化、量化、坐标域索引等，探讨了平均值、标准差的计算及其在信号处理中的意义。文章还分析了信号与基本过程、直方图、概率质量函数、概率密度函数的概念，以及数字噪声的产生原理。
先罗列下我的印象
数字信号处理是一种对信号的处理方式
而信号可以来自任何领域
故在很多领域都有DSP的影子
对不同的信号 要先了解其特性 才能处理 故相关领域的知识是必须的
算法的理解
算法的选择
算法的实现
误差的估计
（待续）
第2章
2.1信号与曲线
数字化 量化
坐标
域
索引（0开始）
2.2平均值和标准差
注意信号的功率特性而不是幅值
功率与幅值的平方成正比
方差:体现偏离的功率
标准差：信号偏离平均值（功率开方）
与平均偏差作对比！！！
RMS 与标准差 （注意直流偏置）
连续统计中的偏差计算方式：[平方和 - 和方/N] / [1-N]
信噪比SRN (平均值与标准差的比)
变异系数CV (1/SRN)
2.3 信号与基本过程
基本过程有着精确的概率
采集信号是在确定的范围内对信号进行统计 其概率是波动的（统计波动 统计起伏）
这种波动有’典型差错‘ 可根据公式求的
标准偏差的估计 和标准偏差 （N-1 与 N）(标准差公式中N-1 是一种误差减小的修正方式)
（
标准差计算需要平均值 而平均值是由统计得出存在误差
当N比较小时直接除N计算标准差会有较大的误差
不稳定态（基本过程的平均值在变）
常见问题：缓慢变化的平均值干扰了标准偏差
解决方法：将信号分小段 分别计算各段的统计值
还可以再将每小段的标准偏差求平均 求出以个全局的标准偏差
）
2.4直方图，概率质量函数，概率密度函数
抽样点数多 图像变得平滑了
（统计噪声与抽样点数的平方成反比 怎么看出来的？？？ ）
使用直方图计算平均值与标准偏差（有点加权平均数的感觉）
平均值
标准偏差
（取值相同的抽样点同时运行）
采集信号的基本过程是叠加了噪声的
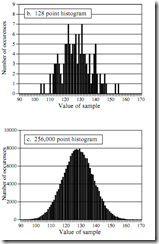
直方图
由采集信号形成
所有值的和与抽样点数相同
概率质量函数
直方图相应的基本过程的曲线（‘轮廓’）被称为 概率质量函数（pmf） （是 离散 的）（只用于离散数据）
pmf 描述某个值出现的概率
需要归一化 （除以抽样点的总数）
归一后 各点的值累加为1
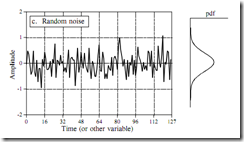
概率密度函数
相对应的在连续信号
出现 概率密度函数（pdf）
归一后面积为1
当抽样级数>>抽样点数 （如浮点数 整数间有各种分数）
分组发解决
组的数量控制着X 与Y 轴的分辨率
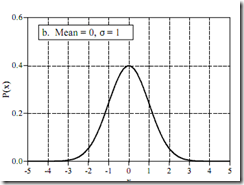
正态分布
标准差：曲线的宽度
平均值：曲线的中心位置
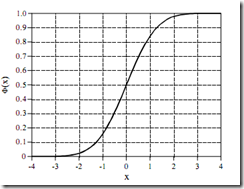
累计分布函数
重负无穷到某数的概率
2.6数字噪声的产生
数字噪声：
核心：随即数生成器
（
0~1分布均匀
平均数：0.5
标准差1/((12)^(`1/2))
）
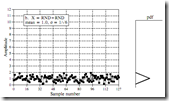
生成流程：
随机信号叠加
（独立随机信号相加，偏差也相加）
扫一扫
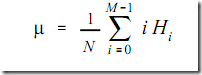
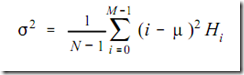
568
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
