软件工程第二次作业——个人项目

一、Github项目地址

• github地址：https://github.com/leijing000/SoftwareEngineering
• 作业地址：https://edu.cnblogs.com/campus/fzu/FZUSoftwareEngineering1715W/homework/866

二、在开始实现程序之前，在PSP表格记录下你估计将在程序的各个模块的开发上耗费的时间。

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30
· Estimate	· 估计这个任务需要多少时间	30
Development	开发	1120
· Analysis	· 需求分析 (包括学习新技术)	540
· Design Spec	· 生成设计文档	60
· Design Review	· 设计复审 (和同事审核设计文档)	40
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30
· Design	· 具体设计	120
· Coding	· 具体编码	300
· Code Review	· 代码复审	30
· Test	· 测试（自我测试，修改代码，提交修改）	150
Reporting	报告	30
· Test Report	· 测试报告	60
· Size Measurement	· 计算工作量	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30
合计		1300

三、解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的心路历程。

   刚开始看到题目时，就感觉好难的样子，完全没有思路，不知从何下手，感觉挺复杂的。最开始就是想在每一格中随机填数，然后再进行验证，感觉要验证的挺多的，很复杂，对数独又比较陌生，就去网上搜了些生成数独的方法。看到了一种变换的方法，感觉没有那么复杂，就是先写出第一个数组，在第一个数组的基础上进行变换，可以左右列进行交换，可以上下行进行交换，还可以不同数字之间进行交换，不同的交换方式增加了数独的随机性，但我觉得这种数独产生的方式随机性不是很好，都是在第一个的基础上变换而来，因此每个数据也会长得极为相似，变换回原来的数独的概率也是蛮大的，当生成很多数独时，就有很大概率会重复，就无法满足题目中不重复的要求。由于每行每列每个九宫格都不会有重复的数字，后来有想过一个数字一个数字地放置，将1从第一行开始放，放到最后一行，把1放完之后再放数字2，感觉这也是可行的，但是位置的选择挺麻烦的，我还没发现它们之间的规律，即每个数字要如何放置在合理的位置，且对接下来数字的影响较小，位置不好找，因此这种想法没有进行尝试。
   后来在网上看到了随机法和回溯法，我都尝试着打了一遍，感觉回溯法效率会高一些。随机法是每个位置都从1-9中随机选一个数放置，再判断是否合理，合理就放置，不合理就将该数删除，在剩下的数中重新找过，这跟我一开始未成形的想法有些相似。当随机法生成数独失败后，将会重新生成数独，这点跟回溯法不一样，如果某个数放置得不合理，可以退回去修改前面的数，使得后面的数变得合理，因此无需重新生成，效率高了许多。

四、设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？

代码总共有一个sudoku类，该类中包含四个函数：

void init();//初始化棋盘
void print();//打印数独棋盘
bool isRightposition(int row, int col);//验证是否可以放置
bool generate(int mark);//生成数独

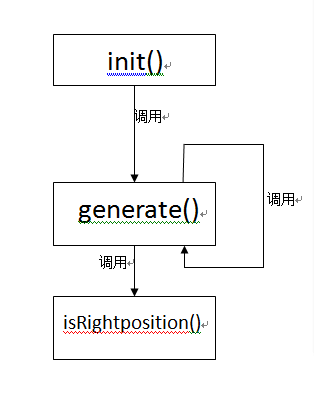
最核心的函数是generate()，在运行过程中它会不断回溯，并判断位置是否合理(isRightpositio()）)。每次生成数独之前都要初始化(init())。

• 以下是各函数之间的流程图：

五、代码说明。展示出项目关键代码，并解释思路与注释说明。

比较核心的代码是isRightposition()和generate()

• isRightposition()代码部分

思路：每填入一个数字都要进行验证，主要验证以下三个方面：
1、同行不同列数字重复;
2、同列不同行数字不能重复;
3、每个九宫格的数字不能重复

bool isRightposition(int row, int col)
{
    int curNum = shudu[row][col];
        //验证行
    for (int i = 0; i < row; i++)
    {
        if (shudu[i][col] == curNum)
        {
            return false;
        }
    }
    //验证列
    for (int i = 0; i < col; i++)
    {
        if (shudu[row][i] == curNum)
        {
            return false;
        }
    }
    //验证九宫格 
    int rowStart = row / 3 * 3;
    int rowEnd = rowStart + 2;
    int colStart = col / 3 * 3;
    int colEnd = colStart + 2;
    for (int i = rowStart; i <= rowEnd; i++)
    {
        for (int j = colStart; j <= colEnd; j++)
        {
            if (shudu[i][j] == curNum && i != row && j != col)
            {
                return false;
            }
        }
    }
}

• generate()代码部分

思路：采用回溯法，将每个格子进行编号，总共0-80。用一个长度为9的数组的0、1状态记录随机数1-9的使用情况。每次随机生成一个下标，判断该下标对应的数是否为0,若不是，表示该下标作为随机数已被用过，重新选择一个随机数，0表示数未被使用过，则将该下标作为随机数赋给数独，之后进行判断，该位置是否合理，合理则继续生成下一个数，不合理则回溯，重新生成上一个数，如此循环，直到mark == 81时表示数独生成完毕。

//采用回溯法，将格子进行编号（0-80）
bool generate(int mark)
{
    if (mark == 81)
    {
        return true;
    }    
    int row = mark / 9;//行坐标
    int col = mark % 9;//列坐标    
    //若当前位置已填入数字，则继续往下生成
    if (shudu[row][col] != 0)
    {
        if (generate(mark + 1))
        {
            return true;
        }
    }
    else
    {
        int count = 0;
        int index;
        //arr用来标记数字是否被使用 ，0表示未用，1表示已用
        int arr[9] = { 0 };
        for (int i = 0; i < 9; i++)
        {
            //生成随机数字，直到1到9全部生成完毕 
            while (1)
            {
                index = rand() % SIZE + 1;
                if (arr[index - 1] == 0)
                {
                    arr[index - 1] = 1;
                    count++;
                    break;
                }
            }
            shudu[row][col] = index;
            //判断赋值是否合法，合法则继续生成下一位置
            if (isRightposition(row, col))
            {
                if (generate(mark + 1))
                {
                    return true;
                }
            }
            else
            {
                //不合法，回溯
                shudu[row][col] = 0;
            }
        }
    }
    return false;
}

六、测试运行。程序必须是可运行的，展示出程序运行的截图。

• 输入不合法的情况

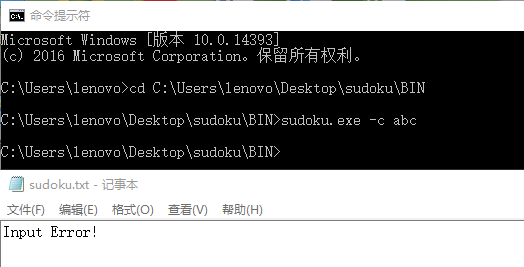
• 运行结果演示

七、记录在改进程序性能上所花费的时间，描述你改进的思路，并展示一张性能分析图，并展示你程序中消耗最大的函数。

之前都没用过性能分析这种东西，完全就是一脸懵逼，看了《构建之法》之后还是没有很清楚，上网搜了一下，也挺混乱的。后来在慢慢的摸索下貌似弄了出来，但也不知道对不对，花了挺多时间的。

• 性能分析

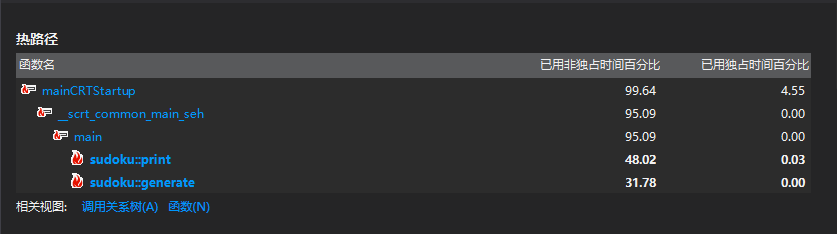
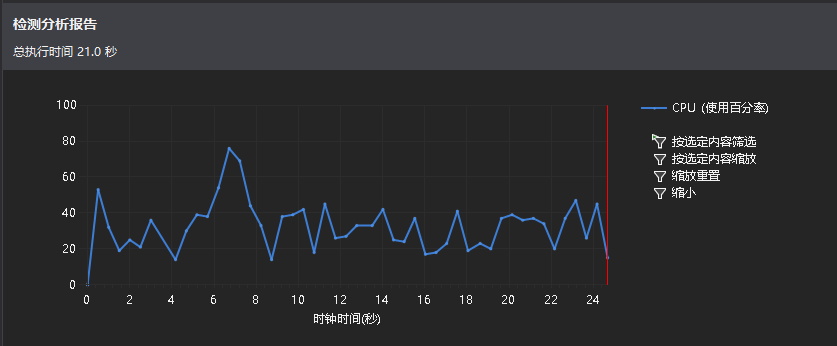
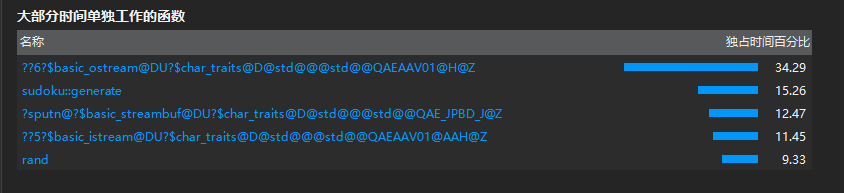
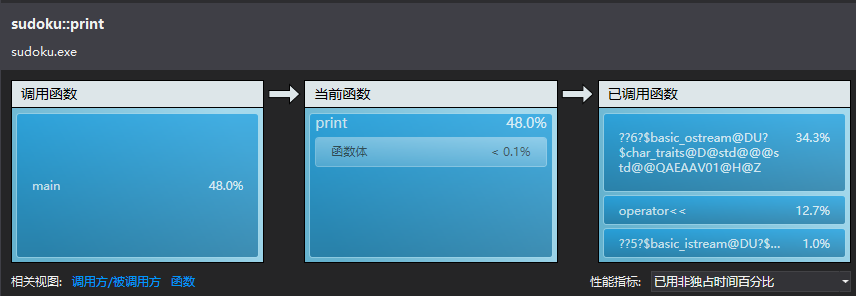
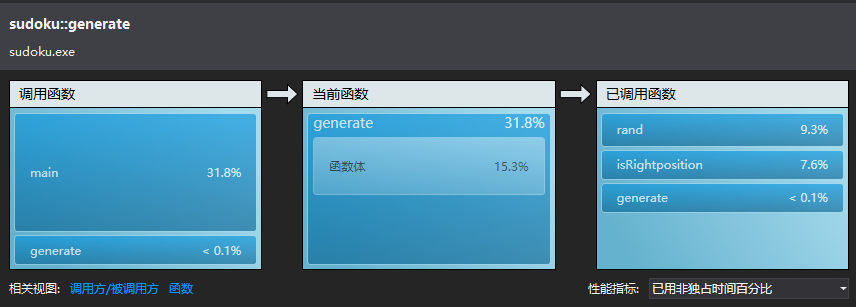
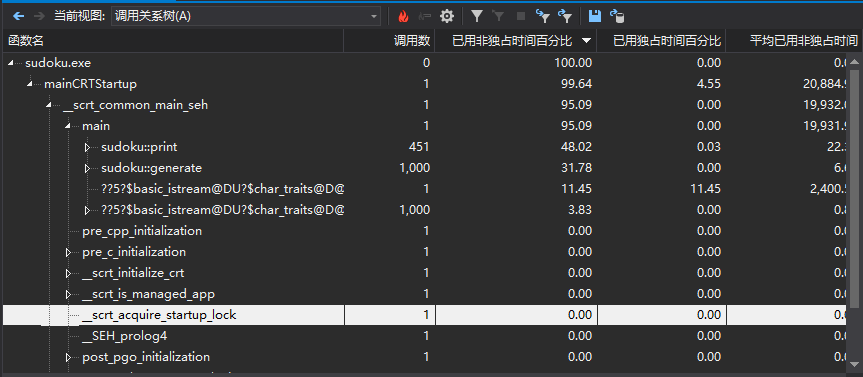
从以上图中可以看出，print()是消耗最大的函数，其次是generate()。跟我预想的不一样，一开始以为generate()会消耗最多，因为要一直循环验证。后来尝试着将输出部分用C来写，感觉速度有快些，但不明显。而且我发现，有些时间偏差还是挺大的，不知道是电脑太卡了还是代码的问题，我觉得最有可能影响运行速度的应该是generate()函数，因为随机数是随机生成的，要一直随机到满足条件位置，我感觉这里的时间是不太稳定的。

• 单元测试

#include "stdafx.h"
#include "CppUnitTest.h"
#include"../sudoku/sudoku.h"    
using namespace Microsoft::VisualStudio::CppUnitTestFramework;    
namespace UnitTest1
{
    TEST_CLASS(UnitTest1)
        {
    public:    
        TEST_METHOD(TestisRightposition)
        {
            // TODO: 在此输入测试代码
            sudoku sudo;
            sudo.init();
            bool pos = sudo.isRightposition(3, 3);
            Assert::IsTrue(pos == false);
        }    
    };
}

八、在你实现完程序之后，在PSP表格记录下你在程序的各个模块上实际花费的时间。

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划		40
· Estimate	· 估计这个任务需要多少时间		40
Development	开发		1390
· Analysis	· 需求分析 (包括学习新技术)		480
· Design Spec	· 生成设计文档		20
· Design Review	· 设计复审 (和同事审核设计文档)		0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)		20
· Design	· 具体设计		200
· Coding	· 具体编码		480
· Code Review	· 代码复审		40
· Test	· 测试（自我测试，修改代码，提交修改）		150
Reporting	报告		110
· Test Report	· 测试报告		40
· Size Measurement	· 计算工作量		30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划		40
合计			1540

总结

   感觉这次作业挺难的，有很多新东西是我从来都没有接触过的，虽然之前也有用VS进行编程，但是从来没有用过性能分析和单元测试。一开始写数独就写了挺久的，传github也出现了一些问题，不过最终还是完成了，感觉自己还是学到了许多东西的，对github的使用更加熟练了，也知道了vs更多的功能，不只是纯粹用来打代码。

转载于:https://www.cnblogs.com/leijing/p/7513069.html