本系列笔记内容参考来源为李航《统计学习方法》
k近邻是一种基本分类与回归方法,书中只讨论分类情况。输入为实例的特征向量,输出为实例的类别。k值的选择、距离度量及分类决策规则是k近邻法的三个基本要素。
k近邻算法
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。
k近邻法没有显示的学习过程。

k近邻模型
距离度量
一般为欧式距离,Lp距离、Minkowski距离等
由不同的距离度量所确定的最近邻点是不同的。

式3.5也称为切比雪夫距离。
夹角余弦
几何中用来衡量两个向量方向的相似度。
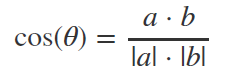
k值的选择
k值小时,k近邻模型更复杂,容易发生过拟合;k值大时,模型更简单。k值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的k。
分类决策规则
常用的分类决策规则是多数表决,对应与经验风险最小化。
k近邻法的实现:kd树
构造kd树算法如下:


搜索kd树即回溯法:


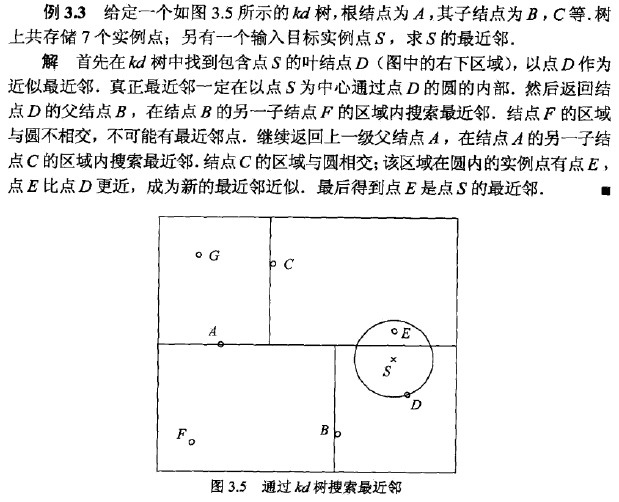




 本文详细介绍了k近邻算法的基本原理,包括k值选择、距离度量和分类决策规则。探讨了不同距离度量对最近邻点的影响,并讨论了k值大小对模型复杂度和过拟合的影响。同时,介绍了k近邻法的实现方法——kd树。
本文详细介绍了k近邻算法的基本原理,包括k值选择、距离度量和分类决策规则。探讨了不同距离度量对最近邻点的影响,并讨论了k值大小对模型复杂度和过拟合的影响。同时,介绍了k近邻法的实现方法——kd树。
















 936
936

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








