20165203 四则运算(第二阶段)总结
一、需求分析
1.通过命令行输入生成题目的数量,随机生成题目。
2.生成的题目不重复。
3.生成的四则运算题目支持整数、支持多运算符。
4.生成的四则运算题目支持真分数。
5.能够根据作答情况统计正确的个数。能够根据作答情况统计正确的个数。
6.能够根据作答情况输出正确率。
二、设计思路
本周的新功能主要是在运算题目可以支持真分数上,所以设计也主要是围绕于此。增加一个类,这个类用来判断是否为真分数。若为真分数,则进入真分数的计算类。若不为真分数,则进入整数的计算类。此外就是我们增加了可以输出正确率的功能,这个就是增加一个变量,它的值为正确的题目个数除以总题目个数即可。
UML图
三、核心代码
1.各运算值的计算:
public class RationalNumber {
private int numerator, denominator;
public RationalNumber(int numer, int denom) {
if (denom == 0)
denom = 1;
if (denom < 0) {
numer = numer * -1;
denom = denom * -1;
}
numerator = numer;
denominator = denom;
reduce();
}
public int getNumerator() {
return numerator;
}
public int getDenominator() {
return denominator;
}
public RationalNumber reciprocal() {
return new RationalNumber(denominator, numerator);
}
public RationalNumber add(RationalNumber op2) {
int commonDenominator = denominator * op2.getDenominator();
int numerator1 = numerator * op2.getDenominator();
int numerator2 = op2.getNumerator() * denominator;
int sum = numerator1 + numerator2;
return new RationalNumber(sum, commonDenominator);
}
public RationalNumber subtract(RationalNumber op2) {
int commonDenominator = denominator * op2.getDenominator();
int numerator1 = numerator * op2.getDenominator();
int numerator2 = op2.getNumerator() * denominator;
int difference = numerator1 - numerator2;
return new RationalNumber(difference, commonDenominator);
}
public RationalNumber multiply(RationalNumber op2) {
int numer = numerator * op2.getNumerator();
int demon = denominator * op2.getDenominator();
return new RationalNumber(numer, demon);
}
public RationalNumber divide(RationalNumber op2) {
return multiply(op2.reciprocal());
}
public boolean isLike(RationalNumber op2) {
return (numerator == op2.getNumerator() && denominator == op2.getDenominator());
}
public String toString() {
String result;
if (numerator == 0)
result = "0";
else if (denominator == 1)
result = numerator + "";
else
result = numerator + "/" + denominator;
return result;
}
private void reduce() {
if (numerator != 0) {
int common = gcd(Math.abs(numerator), denominator);
numerator = numerator / common;
denominator = denominator / common;
}
}
private int gcd(int num1, int num2) {
while (num1 != num2)
if (num1 > num2)
num1 = num1 - num2;
else
num2 = num2 - num1;
return num1;
}
public int compareTo(RationalNumber answer1) {
if (answer1.getDenominator() == this.getDenominator() && answer1.getNumerator() == this.getNumerator())
return 1;
if (answer1.getNumerator() != this.getNumerator() && answer1.getDenominator() != this.getDenominator())
return 0;
else
return Integer.parseInt(null);
}
} 2.计算正确率
num=scan.nextInt();
accuracy = (float)correct/num;
System.out.printf("正确率:%.2f",accuracy*100 );3.利用本周学到的计时器知识,设计了一个计时器代码:
public static void timer1() {
Timer timer = new Timer();
timer.schedule(new TimerTask() {
public void run() {
System.out.println("--请加快操作速度(Quickly)--");
}
}, 5000);// 毫秒
}四、运行截图
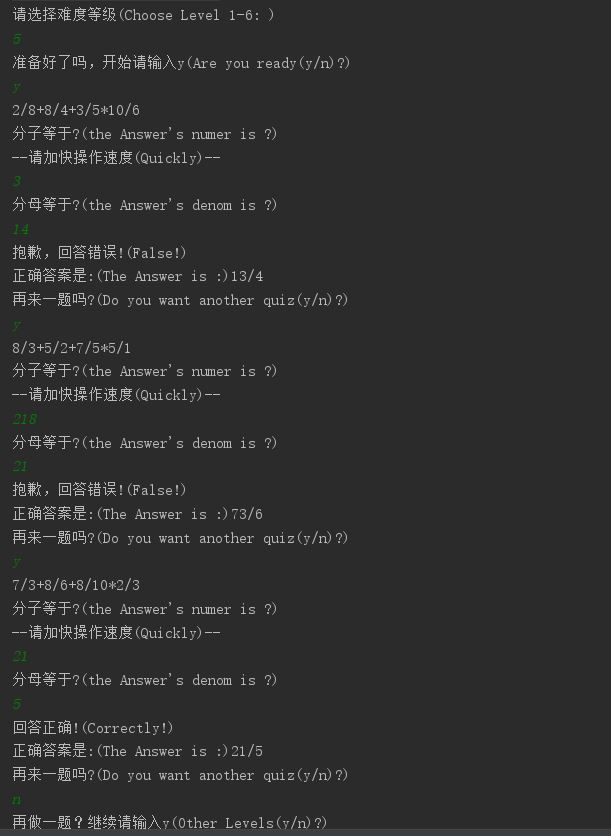

五、结对感想
我的结对伙伴是20165206韩啸,我们设计的成功之处在于设计出了分数的运算,并利用本周学到的计时器的知识设计了一个计时器算法。
六、结对创意图








 本文介绍了四则运算程序的设计与实现,重点讲解了如何处理包含真分数的数学表达式。文章详细阐述了真分数运算的逻辑,并展示了如何计算答题正确率及使用计时器提醒用户等功能。
本文介绍了四则运算程序的设计与实现,重点讲解了如何处理包含真分数的数学表达式。文章详细阐述了真分数运算的逻辑,并展示了如何计算答题正确率及使用计时器提醒用户等功能。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








