一、题目
返回一个二维整数数组中最大联通子数组的和。
二、要求
输入一个二维整型数组,数组里有正数也有负数。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
程序所要使用的数组放在一个input.txt的文件中。
三、设计思想
本次实验设计思路是根据课上同学讲的方法写的,主要是:正数加进来,遇到负数就跳过。
数据好像流水一般,就往正数方向流动并相加,直到取得的最大联通子数组和最大。
四、源代码
//数组04 //胡浩特、朱子嘉 2016/4/5 #include<iostream> #include<ctime> #include<fstream> using namespace std; void main() { int m, n, i, j, sum; int smark, mmark, t2; int up[100], down[100], t[100]; int a[100][100], b[100]; cout << "请输入二维数组的行数:" << endl; cin >> m; cout << "请输入二维数组的列数:" << endl; cin >> n; cout << "请输入二维数组的元素:" << endl; for (i = 0; i<m; i++) { for (j = 0; j<n; j++) { cin >> a[i][j];//输入二维数组的元素 } } for (i = 0; i<m; i++) { for (j = 0; j<n; j++) { b[j] = a[i][j]; } int c[100] = { 0 }; int sum1 = 0, max1 = 0, k; for (k = 0; k<n; k++) //在列上求每一个最大子数组 { if (sum1<0) { sum1 = b[k]; } else { sum1 = sum1 + b[k]; } c[k] = sum1; } max1 = c[0]; for (k = 0; k<n; k++) { if (max1<c[k]) { max1 = c[k]; mmark = k; } } for (k = mmark; k >= 0; k--) { if (c[k] == b[k]) { smark = k; break; } } sum = max1; up[i] = smark; down[i] = mmark; t[i] = sum; } t2 = t[0]; for (i = 0; i + 1<m; i++) { if (up[i] <= down[i + 1] && down[i] >= up[i + 1]) { t2 += t[i + 1]; } for (j = up[i]; j<up[i + 1]; j++) { if (a[i + 1][j]>0) t2 += a[i + 1][j]; //判别独立正数 } } //文件输出 ofstream fout("D:\\input.txt", ios::binary); for (i = 0; i<m; i++) { for (j = 0; j<n; j++) { fout << a[i][j] << " "; } fout << endl; } fout << "最大联通子数组的和为:" << t2 << endl; }
五、实验截图
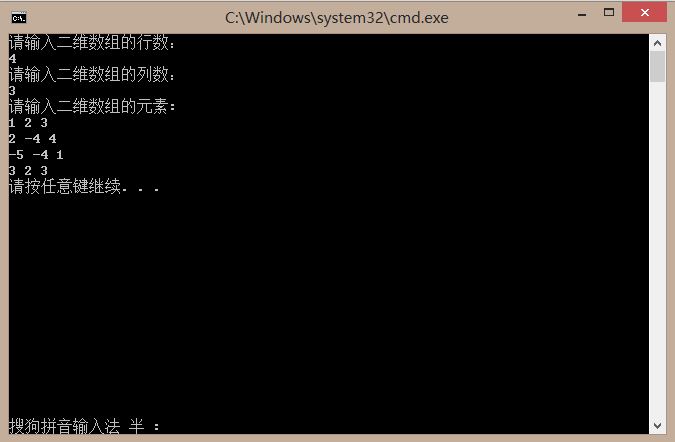
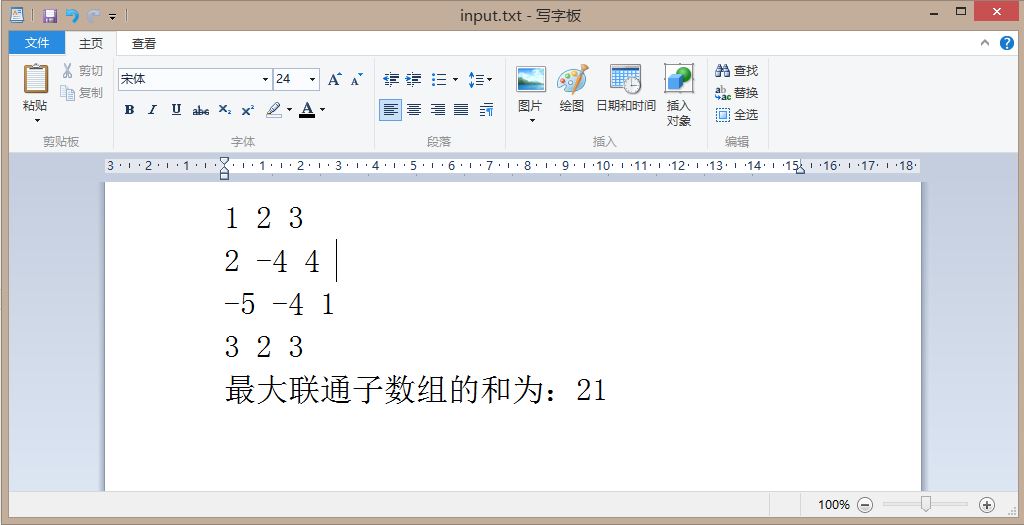




 本文介绍了一种求解二维整数数组中最大联通子数组和的算法,通过正数累加、负数跳过的策略,实现了时间复杂度为O(n)的高效求解方法,并提供了完整的C++实现代码。
本文介绍了一种求解二维整数数组中最大联通子数组和的算法,通过正数累加、负数跳过的策略,实现了时间复杂度为O(n)的高效求解方法,并提供了完整的C++实现代码。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








