bzoj1719 [Usaco2006 Jan] Roping the Field 麦田巨画

1719: [Usaco2006 Jan] Roping the Field 麦田巨画

Time Limit: 5 Sec  Memory Limit: 64 MB
Submit: 80  Solved: 24
[ Submit][ Status][ Discuss]

Description

Farmer John is quite the nature artist: he often constructs large works of art on his farm. Today, FJ wants to construct a giant "field web". FJ's field is large convex polygon with fences along the boundary and fence posts at each of the N corners (1 <= N <= 150). To construct his field web, FJ wants to run as many ropes as possible in straight lines between pairs of non-adjacent fence posts such that no two ropes cross. There is one complication: FJ's field is not completely usable. Some evil aliens have created a total of G (0 <= G <= 100) grain circles in the field, all of radius R (1 <= R <= 100,000). FJ is afraid to upset the aliens, and therefore doesn't want the ropes to pass through, or even touch the very edge of a grain circle. Note that although the centers of all the circles are contained within the field, a wide radius may make it extend outside of the field, and both fences and fence posts may be within a grain circle. Given the locations of the fence posts and the centers of the circles, determine the maximum number of ropes that FJ can use to create his field web. FJ's fence posts and the circle centers all have integer coordinates X and Y each of which is in the range 0..1,000,000.

    约翰真是一个自然派艺术大师，他常常在他的田地上创作一些巨大的艺术杰作．今天，他想在麦田上创作一幅由绳索构成的巨画．他的麦田是一个多边形，由N(1≤N≤150)个篱笆桩和之间的篱笆围成．为了创作他的巨画，他打算用尽量多的数量的绳索，笔直地连接两个不相邻的篱笆桩．但是为了画作的优美，任意两根绳索不得交叉．

    约翰有一个难处：一些邪恶的外星人在他的麦田上整出了G(O≤G≤100)个怪圈．这些怪圈都有一定的半径R(1≤R≤100000)．他不敢惹外星人，所以不想有任何绳索通过这些怪圈，即使碰到怪圈的边际也不行．这些怪圈的圆心都在麦田之内，但一些怪圈可能有部分在麦田之外．一些篱笆或者篱笆桩都有可能在某一个怪圈里．

    给出篱笆桩和怪圈的坐标，计算最多的绳索数．所有的坐标都是[0，10^61内的整数．

Input

* Line 1: Three space-separated integers: N, G, and R * Lines 2..N+1: Each line contains two space-separated integers that are the X,Y position of a fence post on the boundary of FJ's field. * Lines N+2..N+G+1: Each line contains two space-separated integers that are the X,Y position of a circle's center inside FJ's field.

    第1行输入三个整数N，G，R.接下来N行每行输入两个整数表示篱笆桩的坐标．接下来G行每行输入两个整数表示一个怪圈的圆心坐标．

Output

* Line 1: A single integer that is the largest number of ropes FJ can use for his artistic creation.

    最多的线索数．

Sample Input

5 3 1
6 10
10 7
9 1
2 0
0 3
2 2
5 6
8 3

INPUT DETAILS:

A pentagonal field, in which all possible ropes are blocked by three
grain circles, except for the rope between fenceposts 2 and 4.

Sample Output

1

HINT

除了篱笆桩2和4之间可以连接绳索，其余均会经过怪圈

Source

Gold

[ Submit][ Status][ Discuss]

---

大力预处理+区间dp

直接先预处理哪些绳索是和怪圈有交的

ok[l][r]表示l和r能否连绳索

这里有一个细节就是圆不在线段上方时

就要判断圆心和端点的距离否则时圆心和线段所在直线的距离

因为给出的是一个凸包

观察可得 如果选取了绳索(l,r)那么区间[l,r]里的点不能再向外连边了

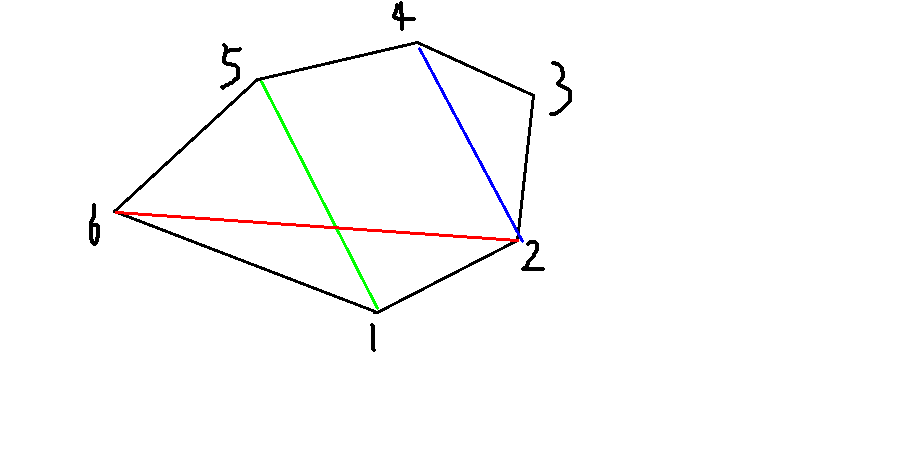
绿色的边表示已经连了 1和5

红色表示2和6不能连

蓝色表示2和4还可以连

所以可以区间dp

f[l][r]=max(f[l][m]+f[m][r])+ok[l][r]

代码:

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Rep(i,x,y) for(int i=x;i<y;++i)
#define For(i,x,y) for(int i=x;i<=y;++i)
using namespace std;
const int N = 1000;
const double eps = 1e-10;
int n,g,r;
struct pts{
    long long x,y;
    inline void rd(){
        scanf("%lld%lld",&x,&y);
    }
    pts operator - (pts b) {
        return (pts){x-b.x,y-b.y};
    }
    long long operator ^ (pts b) {
        return x*b.y-y*b.x;
    }
    long long operator * (pts b) {
        return x*b.x+y*b.y;
    }
};
struct line{
    pts a,b;
};
double DIS(const pts&a,const pts&b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
pts p[N],c[N];
int f[N][N];
bool vis[N][N];
bool ok[N][N];
bool cmp(pts a,pts b){
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
bool CMP(pts a,pts b){
    return ((a-p[1])^(b-p[1]))>0;
}
bool ck(line l,pts p){
    pts ab=l.b-l.a;
    pts ba=l.a-l.b;
    if((ab*(p-l.a))<0)
        return DIS(p,l.a)<=r+eps;
    if((ba*(p-l.b))<0)
        return DIS(p,l.b)<=r+eps;
    long long K=(l.b-l.a)^(p-l.a);
    if(K<0) K=-K;
    return K/DIS(l.a,l.b)<=r+eps;
}
bool OK(line l){
    For(i,1,g) if(ck(l,c[i])) return 0;
    return 1;
}
int dp(int l,int r){
    if(l==r||vis[l][r]) return f[l][r];
    vis[l][r]=1;
    Rep(m,l+1,r)
        f[l][r]=max(f[l][r],dp(l,m)+dp(m,r));
    f[l][r]+=ok[l][r];
    return f[l][r];
}
int main(){
    scanf("%d%d%d",&n,&g,&r);
    For(i,1,n) p[i].rd();
    sort(p+1,p+n+1,cmp);
    sort(p+2,p+n+1,CMP);
    For(i,1,g) c[i].rd();
    For(i,1,n){
        For(j,i+2,n){
            if(i==1&&j==n) continue;
            ok[i][j]=OK((line){p[i],p[j]});
        }
    }
    printf("%d\n",dp(1,n));
    return 0;
}

 

转载于:https://www.cnblogs.com/rwy233/p/6946507.html