树状数组板子

 

　大杀器 树状数组,可以降低复杂度O(M*N)到O(M*lgN)

　通过数据 i 的二进制数,进行分块

 

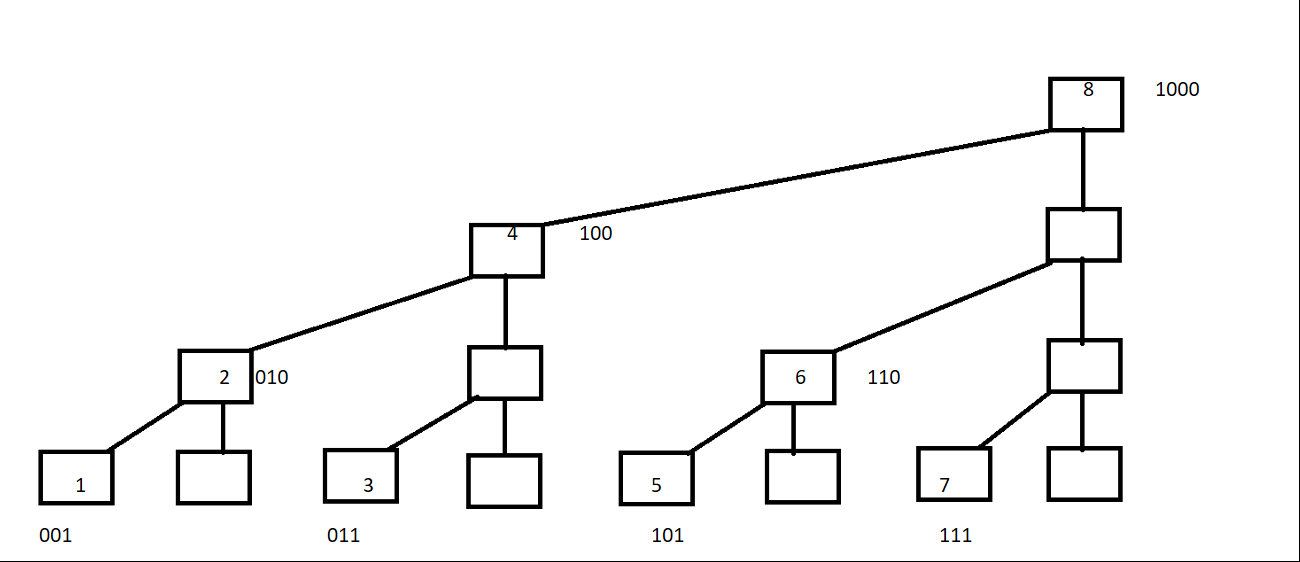
C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

 

 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll ;
typedef double    dl ;
#define INF 0x7f

const int inf = 987654321;
const int sz = 1e4 + 5;
const int mod = 1e9 + 7;
const int sqrtn = 300;

#define f(i,l,r) for(int i=l;i<=r;++i)
#define g(i,l,r) for(int i=l;i>=r;--i)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
#define pii pair<int,int>
#define lowbit(x) x&(-x)
#define X first
#define Y second
int n,m,op,s1,e1,s2,e2;
int bits[sz][sz],a[sz][sz];
void update(int l,int r,int k)
{
    for(int i=l;i<=n;i+=lowbit(i))
        for(int j=r;j<=n;j+=lowbit(j))
            bits[i][j]+=k;
}
int query(int l,int r)
{
    int ans=0;
    for(int i=l;i;i-=lowbit(i))
        for(int j=r;j;j-=lowbit(j))
            ans+=bits[i][j];
    return ans;
}

 

转载于:https://www.cnblogs.com/corx/p/8472585.html