矩阵快速幂求Fibonacci

最新推荐文章于 2025-04-23 17:31:32 发布

转载最新推荐文章于 2025-04-23 17:31:32 发布 · 46 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/bennettz/p/7644417.html

本文介绍了一种使用矩阵快速幂算法高效计算斐波那契数列的方法。通过定义特定的矩阵并利用快速幂运算，可以大幅度减少计算复杂度，实现O(log n)的时间复杂度内求解第n项斐波那契数。

原理

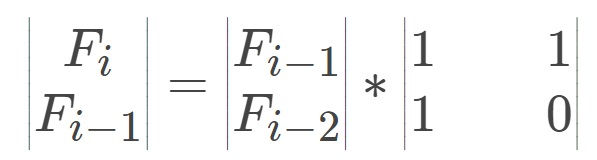
我们取矩阵A

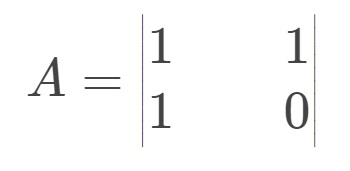
则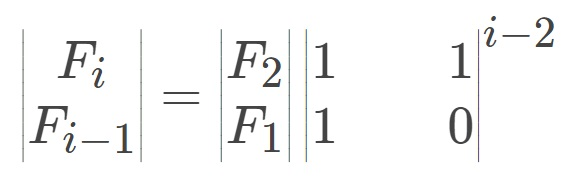

F1=F2=1;则可以轻易求出F(i)

#define maxn 2
#define mo 1000000007
struct Matrix{
    long long a[maxn][maxn];
    Matrix(){
        memset(a,0,sizeof(a));
    }
    Matrix operator * (const Matrix& c)const{
        Matrix b;
        for(int i=0;i<maxn;i++){
            for(int j=0;j<maxn;j++){
                for(int k=0;k<maxn;k++){
                    b.a[i][j]+=a[i][k]*c.a[k][j];
                    b.a[i][j]%=mo;
                }
            }
        }
        return b;
    }
}a;
Matrix power(Matrix a,long long b){//a^b%mo
    Matrix ans;ans.a[0][0]=ans.a[1][1]=1;
    while(b){
        if(b&1)ans=ans*a;
        a=a*a,b>>=1;
    }
    return ans;
}
long long Fibonacci(long long x){
    if(x<2)return 1;
    Matrix b=power(a,x-2);
    return b.a[0][0]+b.a[1][0];
}