本章目的:明确公差分布(Tolerance Distribution)也有自己的形状,了解CPK概念。
1.正态分布(常态分布)normal distribution的概念
统计分析常基于这样的假设:零件在大批量生产时,其尺寸在其公差范围内呈正态分布(常态分布)normal distribution。
事实也是如此,针对一个零件尺寸,在一定制造条件下制造并测量无数个零件,并记录相同尺寸出现的频率,可以绘制出一张尺寸大小的频率图,这张图纸就是正态分布图。如下面两张图所示(一简一繁)。
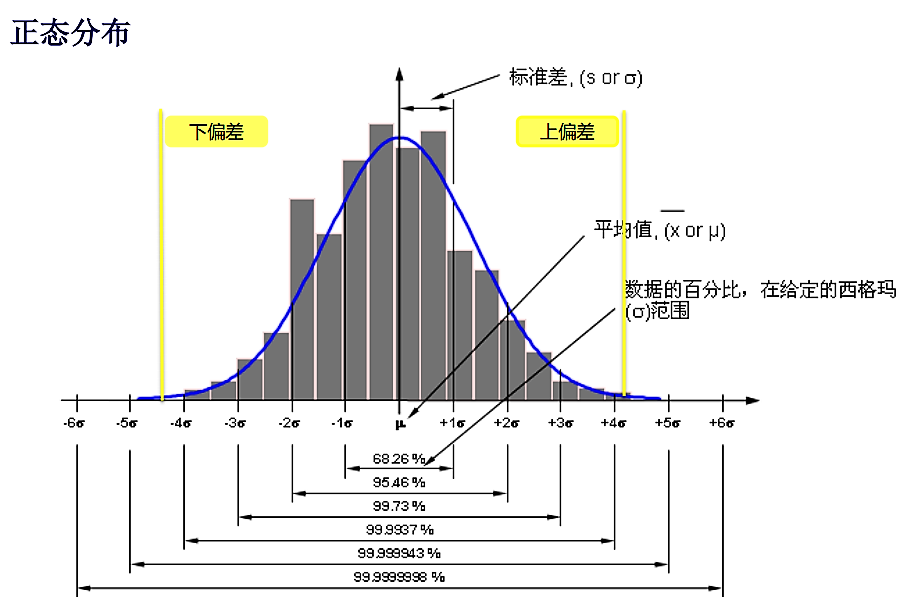
多数的零件尺寸值会向着图形的中心,即尺寸的平均值聚集,离平均值越远,该尺寸出现的可能性就越小。
这里就有两个重要值,中间值μ与标准差σ。即公差形状的中心和范围,各本书中关于这两个值的解释和标注都有所不同,但工程师要注意其本质。
中间值μ:曲线对称轴的位置,这决定了整条曲线的位置。
标准差σ:由中间值到曲线的曲率正负号改变点的距离,这决定了曲线的分散或集中程度。
补充解释如下图(spc手册):
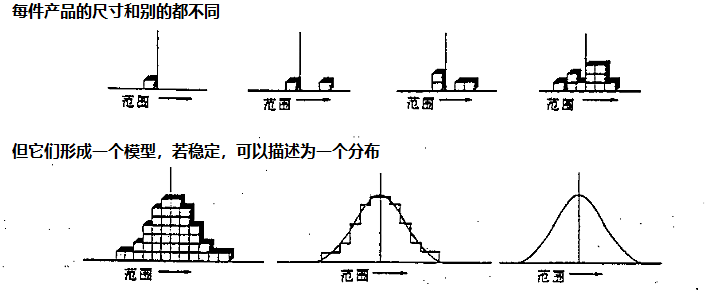
正态分布,即是公差的形状,需要熟记于心。
从正态分布的概念看出,图纸公差标注只代表的是范围值,却不能规定制造零件的合格率形状。
所以我们在图纸绘制时,标注的公差并不能约束它的分布形态。但标注时就需要了解统计分析,遵守基本的公差分布情况。
比如单边公差标注,如1(+0.5/0)等,并不能约束所有制造的零件尺寸又在你的公差范围内,同时又偏向一边,不合理的。如下图:
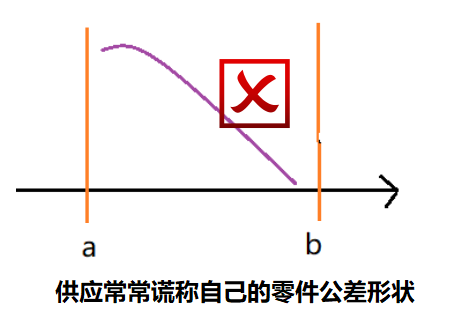
很多供应商声明它们在制作零件时既能保证尺寸在[a,b]范围以内,又能保证大部分的零件靠近a值。这并不符合正态分布的概念。
供应商会告诉你他能做到很多事情,却常常隐瞒你要付出的代价。
1.1 各种公差分布(Tolerance Distribution)的形态
公差分布型态(Tolerance Distribution)不只是一种。如下图所示:
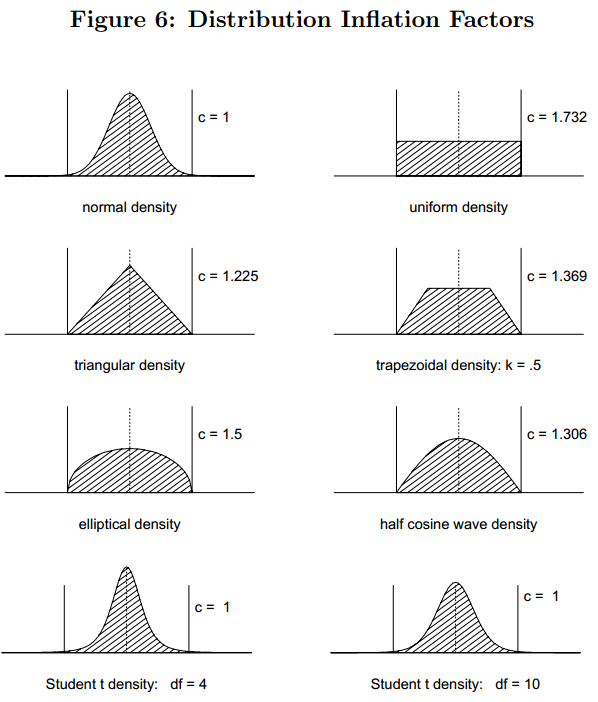





 本文介绍了正态分布的概念及其在公差分析中的应用,强调了理解正态分布对于质量和成本控制的重要性。CPK作为衡量制程能力的指标,依赖于正态分布,用于评估生产过程中尺寸或特性的一致性。文章讨论了CPK、Ca和Cp的关系,并提供了评级标准和处理方法。
本文介绍了正态分布的概念及其在公差分析中的应用,强调了理解正态分布对于质量和成本控制的重要性。CPK作为衡量制程能力的指标,依赖于正态分布,用于评估生产过程中尺寸或特性的一致性。文章讨论了CPK、Ca和Cp的关系,并提供了评级标准和处理方法。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2979
2979

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








