lintcode-119-编辑距离

最新推荐文章于 2025-08-21 10:38:03 发布

转载最新推荐文章于 2025-08-21 10:38:03 发布 · 122 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/libaoquan/p/7208623.html

文章标签：

#数据结构与算法

本文详细介绍了如何通过动态规划解决编辑距离问题，即计算将一个字符串转换为另一个字符串所需的最少操作次数，包括插入、删除和替换操作。文章提供了一个C++实现示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

119-编辑距离

给出两个单词word1和word2，计算出将word1 转换为word2的最少操作次数。
你总共三种操作方法：

插入一个字符
删除一个字符
替换一个字符

样例

给出 work1="mart" 和 work2="karma"
返回 3

标签

字符串处理动态规划

思路

使用动态规划，用二维数组dp[i][j]表示第一个字符串到i第二个字符串到j的时候需要进行多少次修改
动态转移方程为：
dp[i][j] = dp[i-1][j-1] + dp[i-1][j] （S[i]==T[j]）
dp[i][j] = dp[i-1][j] （S[i]!=T[j]）
过程如下：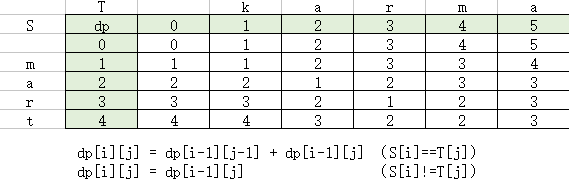

code

class Solution {
public:    
    /**
     * @param word1 & word2: Two string.
     * @return: The minimum number of steps.
     */
    int minDistance(string word1, string word2) {
        // write your code here
        int size1 = word1.size(), size2 = word2.size(),i = 0, j = 0;
        if(size1 <= 0 ) {
            return size2;
        }
        else if(size2 <= 0) {
            return size1;
        }

        vector<vector<int> > dp(size1+1, vector<int>(size2+1, 0));
        for(i=1; i<=size1; i++) {
            dp[i][0]= i;
        }
        for(i=1; i<=size2; i++) {
            dp[0][i] = i;
        }
        for(i=1; i<=size1; i++) {
            for(j=1; j<=size2; j++) {
                if(word1[i-1] == word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                }
                else {
                    dp[i][j] = findMin(dp[i-1][j-1], dp[i][j-1], dp[i-1][j])+1;
                }
            }
        }
        
        return dp[size1][size2];
    }
    
    int findMin(int num1, int num2, int num3) {
        int min = num1 > num2 ? num2 : num1;
        return min > num3 ? num3 : min;
    }
};

转载于:https://www.cnblogs.com/libaoquan/p/7208623.html