140705010001 朱晓秋 第五次作业

 

 

 

 

 

 

 

 

3-3 证明：I(X;Y)=H(X)-H(X|Y)

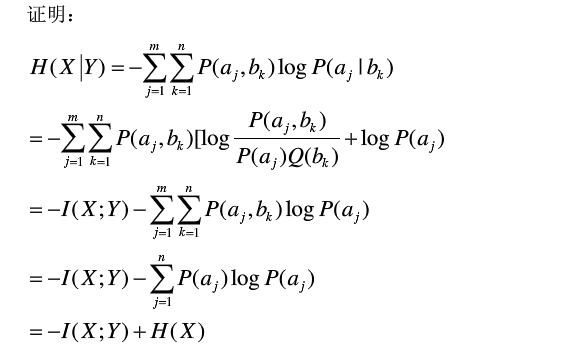
3-9 没有冗余的信源还能不能压缩？为什么？

答：能，不能进行无损压缩，可以进行有损压缩。

3-12 等概率分布的信源还能不能压缩？为什么？你能举例说明吗？

答：至少可以有损压缩。另外，“等概”未必“不相关”，例如对方波信号或锯齿波信号的均匀取样值和对三角波信号的均匀取样值。

3-15 有人认为：“图像的负片（黑白颠倒）比正片更容易压缩”。你同意他的观点吗？为什么？

答：不同意，图像的负片和正片的熵是相同的。

3-16 有人认为：“相关的信源是非等概率分布的”。你同意他的观点吗？为什么？

答：不同意，因为“等概”未必“不相关”、“不等概”未必“相关”。非等概率分布能说明存在冗余度，能够进行压缩，能得出该信源是非等概率分布的。

 

转载于:https://www.cnblogs.com/zhuxiaoqiu/p/6103132.html