挑子学习笔记：两步聚类算法（TwoStep Cluster Algorithm）——改进的BIRCH算法

    转载请标明出处：http://www.cnblogs.com/tiaozistudy/p/twostep_cluster_algorithm.html

    两步聚类算法是在SPSS Modeler中使用的一种聚类算法，是BIRCH层次聚类算法的改进版本。可以应用于混合属性数据集的聚类，同时加入了自动确定最佳簇数量的机制，使得方法更加实用。本文在学习文献[1]和“IBM SPSS Modeler 15 Algorithms Guide”的基础上，融入了自己的理解，更详尽地叙述两步聚类算法的流程和细节。阅读本文之前需要先行学习BIRCH层次聚类算法和对数似然距离。

    两步聚类算法，顾名思义分为两个阶段：

    1）预聚类（pre-clustering）阶段。采用了BIRCH算法中CF树生长的思想，逐个读取数据集中数据点，在生成CF树的同时，预先聚类密集区域的数据点，形成诸多的小的子簇（sub-cluster）。

    2）聚类（clustering）阶段。以预聚类阶段的结果——子簇为对象，利用凝聚法（agglomerative hierarchical clustering method），逐个地合并子簇，直到期望的簇数量。

    两步聚类算法的关键技术如图所示：

 

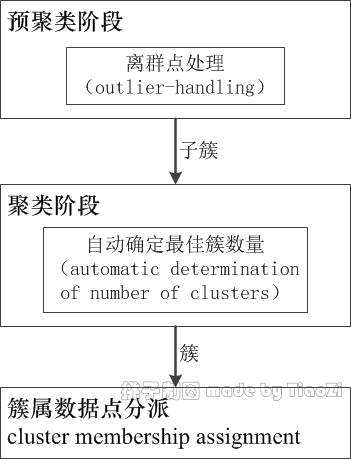
图 1：两步聚类算法的关键技术及流程

    设数据集$\mathfrak D $中有$N $个数据对象/数据点$\{ \vec x_n: n=1,...,N\} $，每个数据对象由$D $个属性刻画，其中有$D_1 $个连续型属性（continuous attribute）和$D_2 $个分类型属性（categorical attribute），设$\vec x_n = (\tilde x_{n1}, ..., \tilde x_{nD_1}, \ddot x_{n1},..., \ddot x_{nD_2}) $，其中$\tilde x_{ns} $表示第$n $个数据对象在第$s $连续型属性下的属性值，$\ddot x_{nt} $表示第$n $个数据对象在第$t $分类型属性下的属性值，已知第$t $个分类型属性有$\epsilon_t $种可能取值。$\mathbf C_J = \{C_1,...,C_J\} $表示对数据集$\mathfrak D $的簇数为$J $的聚类，其中$C_j $表示聚类$\mathbf C_J $中第$j $个簇，不失一般性，设簇$C_j $中有$N_j $个数据对象，$ \{\vec x_{jn}: n=1,...,N_j\} $．

1、预聚类阶段

    在本阶段，首先逐个将数据集$\mathfrak D $中数据点，插入到聚类特征树（CF树）中，实现CF树的生长；当CF树的体积超出设定尺寸时，先剔除当前CF树上的潜在离群点，而后增加空间阈值并对CF树进行瘦身（rebuilding），再将不增加瘦身后的CF树体积的离群点插入CF树中；当遍历所有数据点后，不能插入CF树中的潜在离群点即为真正离群点；最后将最终CF树叶元项（leaf entry）对应子簇的聚类特征输出至算法的下一阶段。本阶段的流程见下图：

 

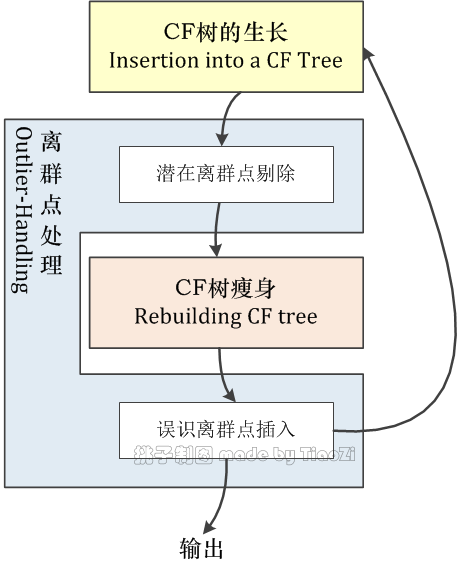
图 2：预聚类阶段流程

1.1 聚类特征

    首先，与BIRCH算法相同，定义簇$\mathfrak D $（也可以是任意的若干个数据点的集合）的聚类特征（cluster feature）：