LeetCode 52.N-Queens II-优快云博客

博客围绕 804. N - 皇后 II 问题展开，该问题是将 n 个皇后置于 n×n 棋盘且彼此不能攻击，需返回不同解决方案数量。解题思路是从第一行第一列开始放皇后，一行一行放置，若某行不能放则回溯，放置到最后一行则计数加一。

804. N-Queens II（N 皇后 II）

题目：

　　n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

　　给定一个整数 n，返回 n 皇后不同的解决方案的数量。

　　示例:

　　输入: 4
　　输出: 2
　　解释: 4 皇后问题存在如下两个不同的解法。
　　[
　　 [".Q..",  // 解法 1
 　　 "...Q",
 　　 "Q...",
　　  "..Q."],

 　　["..Q.",  // 解法 2
 　　 "Q...",
 　　 "...Q",
 　　 ".Q.."]
　　]

思路：

　　这题思路较清晰，先在第一行第一列放置皇后，之后第二行寻找可以放皇后的地方，一行一行放置，如果哪一行不能放置，那么就回溯到上一行，如果放置到了最后一行，那么就代表这种情况成立，计数加一，返回之前一步。

图解：

　　从左上角开始，line1是正对角线，line2是斜对角线，col是竖列。

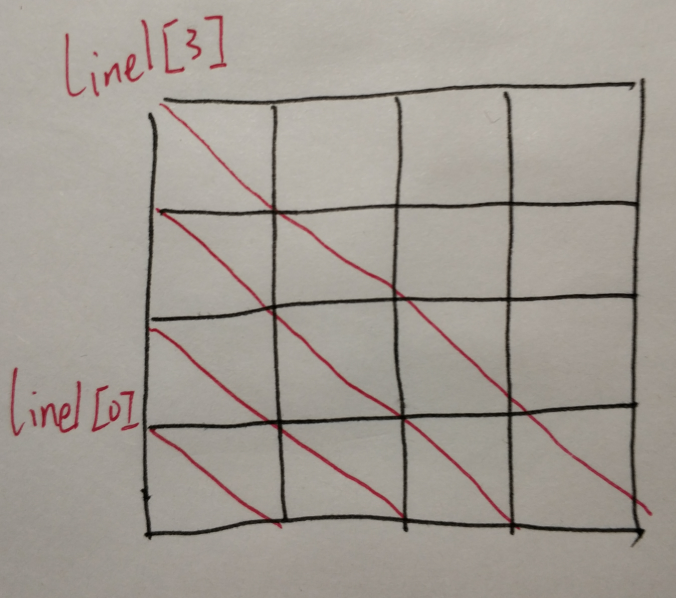
代码：

 1     //列
 2     private static boolean col[];
 3 
 4     //正对角线 x-y+n-1
 5     private static boolean line1[];
 6 
 7     //斜对角线 x+y
 8     private static boolean line2[];
 9 
10     public static int totalNQueens(int n) 
11     {
12         col = new boolean[n];
13         line1 = new boolean[2 * n - 1];
14         line2 = new boolean[2 * n - 1];
15         return putQueen(n, 0);
16     }
17 
18     private static int putQueen(int n, int index) 
19     {
20         int flag = 0;
21         if (index == n) 
22             return 1;
23       
24         for (int i = 0; i < n; i++) 
25         {
26             if (!col[i] && !line1[i - index + n - 1] && !line2[i + index]) 
27             {
28 
29                 col[i] = true;
30                 line1[i - index + n - 1] = true;
31                 line2[i + index] = true;
32                 flag = flag + putQueen(n, index + 1);
33 
34                 col[i] = false;
35                 line1[i - index + n - 1] = false;
36                 line2[i + index] = false;
37             }
38         }
39         return flag;
40     }