1.第一题的核心思想就是一个简单的动态规划,即a[i]+=a[i-1]>0?a[i-1]:0;
但是这样只算成功了一半,我们要做的不是一道题,而是一个普通人可以用的程序。
而要把它编译成可执行文件,就要考虑很多边界因素,比如
(1)输入了几个参数?在这道题中只允许输入一个参数,就是文件名;
(2)输入的是不是合法的文件名;
(3)文件里的数据是否正确;
(4)程序是否有能力处理文件中的数据。
因此,我在前面加了很多的逻辑判断。
之前老师说道了代码覆盖率的问题,可能一条正确的指令加一个正确的文件的代码覆盖率很小,但是防患于未然。
(之前我一直以为覆盖率是说代码的紧凑程度,所以这个代码有点紧凑。。。)
1 #include<stdio.h> 2 int FindMax(int a[],int column) 3 { 4 int max=-1<<31,i; 5 max=a[0]; 6 for(i=1;i<column;i++){ 7 a[i]+=a[i-1]>0?a[i-1]:0; 8 max=max>a[i]?max:a[i];} 9 return max; 10 } 11 int main(int argc,char* argv[]) 12 { 13 if(argc==1){ 14 printf("请在maxsun.exe后输入文件名\n");return -1;} 15 else if(argc>2){ 16 printf("请在maxsun.exe后输入文件名,此为1.0版本,不支持任何附加参数\n");return -1;} 17 else{ 18 if(freopen(argv[1],"r",stdin)==NULL){ 19 printf("文件不存在,请尝试输入文件的完整路径\n");return -1;} 20 int row,column,i=0,a[1000],maxsum; 21 if(scanf("%d",&row)!=1){ 22 printf("文本格式错误,请参照示例输入测试文本(行错误)\n");return -1;} 23 getchar();getchar(); 24 if(scanf("%d",&column)!=1){ 25 printf("文本格式错误,请参照示例输入测试文本(列错误)\n");return -1;} 26 getchar(); 27 while(i<column){ 28 getchar(); 29 if(scanf("%d",&a[i++])!=1){ 30 printf("文本格式错误,请参照示例输入测试文本(数据与行列数不对应)\n");return -1;} 31 if(i>=1000){ 32 printf("数组越界,最多只能处理1000个数\n");return -1;}} 33 maxsum=FindMax(a,column); 34 printf("%d\n",maxsum); 35 fclose(stdin);} 36 return 0; 37 }
测试结果如下:
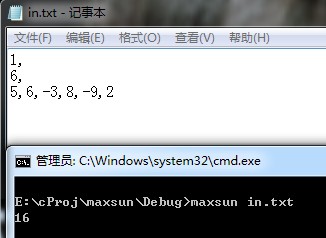
复杂度:O(n)
2.第二题跟第一题的区别就是变成了二维的,那我们只需要开一个一维的数组,枚举我们从文件中得到的二维数组的上下边界,然后将上下边界其中的元素都纵向相加,载入一位数组,这样问题就变回了第一题。
枚举上下界的时候最好一维数组中的临时数据可以重复使用,否则枚举上下界再压扁二维数组的复杂度就已经达到了O(M^3),接下来再找最大,复杂度就成了O(M^3*N)了。
1 #include<stdio.h> 2 #include<string.h> 3 int FindMax(int a[],int column) 4 { 5 int max,i; 6 int b[100]; 7 for(i=0;i<column;i++) 8 b[i]=a[i]; 9 max=b[0]; 10 for(i=1;i<column;i++) 11 { 12 b[i]+=(b[i-1]>0?b[i-1]:0); 13 if(max<b[i]) 14 max=b[i]; 15 } 16 return max; 17 } 18 int main(int argc,char* argv[]) 19 { 20 if(argc==1) 21 { 22 printf("请在maxsun.exe后输入文件名\n"); 23 return -1; 24 } 25 else if(argc>2) 26 { 27 printf("请在maxsun.exe后输入文件名,此为2.0版本,不支持任何附加参数\n"); 28 return -1; 29 } 30 else 31 { 32 if(freopen(argv[1],"r",stdin)==NULL) 33 { 34 printf("文件不存在,请尝试输入文件的完整路径\n"); 35 return -1; 36 } 37 int row,column; 38 if(scanf("%d",&row)!=1) 39 { 40 printf("文本格式错误,请参照示例输入测试文本(行错误)\n"); 41 return -1; 42 } 43 if(row>100) 44 { 45 printf("行数超过限制,最多可允许100行\n"); 46 return -1; 47 } 48 getchar();getchar(); 49 if(scanf("%d",&column)!=1) 50 { 51 printf("文本格式错误,请参照示例输入测试文本(列错误)\n"); 52 return -1; 53 } 54 if(column>100) 55 { 56 printf("列数超过限制,最多可允许100列\n"); 57 return -1; 58 } 59 getchar();getchar(); 60 int i,j; 61 int a[100][100]; 62 memset(a,0,sizeof(a)); 63 for(i=0;i<row;i++) 64 for(j=0;j<column;j++) 65 { 66 if(scanf("%d",&a[i][j])!=1) 67 { 68 printf("文本格式错误,请参照示例输入测试文本(数据与行列数不对应)\n"); 69 return -1; 70 } 71 getchar(); 72 } 73 int up,down; 74 int temp[100]; 75 int record,maxsum=-1<<31; 76 for(up=0;up<row;up++) 77 { 78 memset(temp,0,sizeof(temp)); 79 for(down=up;down<row;down++) 80 { 81 for(j=0;j<column;j++) 82 temp[j]+=a[down][j]; 83 record=FindMax(temp,column); 84 if(record>maxsum) 85 maxsum=record; 86 } 87 } 88 printf("%d\n",maxsum); 89 fclose(stdin);} 90 return 0; 91 }
每个大括号占一行!这样比第一题看起来爽多了有木有。。。
测试结果:
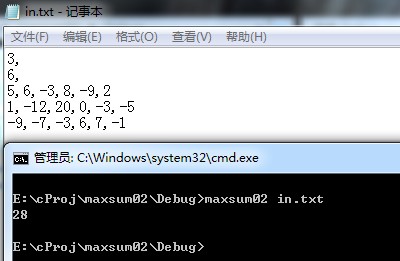
复杂度:O(M^2*N)
3.这个题太难了。以我的能力代码无法实现。
但是我想说说我对此题的看法。
(1)我首先想到的是回溯,但是之前的一维只要前面小于0就可以放弃,但是这个联通的话就无法压成一维,小于0也不能放弃。完全没有剪枝的条件。这样的无脑回溯我认为肯定是行不通的。
(2)第二个想法其实跟第一个想法差不多,这是回溯的时候先强力减一次枝,只要这个元素小于0就不要他,这样我们就得到了独立分散的若干个正数团。然后我们就可以找他们之间需要联通的最小代价,但是我发现找最小代价我也不会。
(3)第三个想法是一个二维的动态规划,因为我们在一维时用到的思想是以a[i]为终点(即a[i]以左)的最大子串,那把这个想法应用到二维,也去找以a[i][j]为终点的最大联通串,即a[i][j]以左以上的整个二维数组的最大联通串。
这个动态规划的方程应该是
a[i][j]=max(a[i-1][j-1]+...,a[i][j-1]+...,a[i-1][j]+...)
其中的...就是以a[][]为终点的最大联通区域的边界向右向下延伸一个单位所增加的数,并且这些数形成了之后的边界。
这个要用好多标记函数,无从下手。
(4)这个想法是我认为最接近正确解法的,就是我们先把每个横向的一维的数据都算出来,在每个a[i]中存放以他为终点的最大子串和以及起始位置,然后我们再纵向算一遍最大子串和,这样找到的最大子串可能就是要求的数了。
4.第四题跟第二题的区别就是加了个参数,在第二题的基础上,我们只需要识别出有效的参数,并对参数做出正确的反应即可。
1 #include<stdio.h> 2 #include<string.h> 3 int flag=0; 4 int maxsum=-1<<31; 5 int a[100][100]; 6 int FindMax(int a[],int column) 7 { 8 int max,i; 9 int b[100]; 10 for(i=0;i<column;i++) 11 b[i]=a[i]; 12 max=b[0]; 13 for(i=1;i<column;i++) 14 { 15 b[i]+=(b[i-1]>0?b[i-1]:0); 16 if(max<b[i]) 17 max=b[i]; 18 } 19 return max; 20 } 21 void Find2DMax(int row,int column) 22 { 23 int up,down,j; 24 int downBoundry=row; 25 int temp[100]; 26 int record; 27 for(up=0;up<row;up++) 28 { 29 memset(temp,0,sizeof(temp)); 30 if(flag==2) 31 downBoundry=up+row; 32 for(down=up;down<downBoundry;down++) 33 { 34 for(j=0;j<column;j++) 35 temp[j]+=a[down%row][j]; 36 record=FindMax(temp,column); 37 if(record>maxsum) 38 maxsum=record; 39 } 40 } 41 } 42 43 int main(int argc,char* argv[]) 44 { 45 if(argc==1) 46 { 47 printf("请在maxsun.exe后输入文件名\n"); 48 return -1; 49 } 50 else if(argc>3) 51 { 52 printf("此为3.0版本,仅支持一位参数:\n\t“/h”(水平相连)或“/v”(垂直相连)\n"); 53 return -1; 54 } 55 else 56 { 57 if(argc==3) 58 { 59 if(*argv[1]=='/'&&*(argv[1]+1)=='h') 60 flag=1; 61 else if(*argv[1]=='/'&&*(argv[1]+1)=='v') 62 flag=2; 63 else{ 64 printf("无效的参数\n"); 65 return -1; 66 } 67 } 68 if(freopen(argv[argc-1],"r",stdin)==NULL) 69 { 70 printf("文件不存在,请尝试输入文件的完整路径\n"); 71 return -1; 72 } 73 int row,column; 74 if(scanf("%d",&row)!=1) 75 { 76 printf("文本格式错误,请参照示例输入测试文本(行错误)\n"); 77 return -1; 78 } 79 if(row>100) 80 { 81 printf("行数超过限制,最多可允许100行\n"); 82 return -1; 83 } 84 getchar();getchar(); 85 if(scanf("%d",&column)!=1) 86 { 87 printf("文本格式错误,请参照示例输入测试文本(列错误)\n"); 88 return -1; 89 } 90 if(column>100) 91 { 92 printf("列数超过限制,最多可允许100列\n"); 93 return -1; 94 } 95 getchar();getchar(); 96 int i,j; 97 memset(a,0,sizeof(a)); 98 for(i=0;i<row;i++) 99 for(j=0;j<column;j++) 100 { 101 if(scanf("%d",&a[i][j])!=1) 102 { 103 printf("文本格式错误,请参照示例输入测试文本(数据与行列数不对应)\n"); 104 return -1; 105 } 106 getchar(); 107 } 108 Find2DMax(row,column); 109 printf("%d\n",maxsum); 110 fclose(stdin); 111 } 112 return 0; 113 }
在这里我把Find2DMax(找二维最大)也从main函数里分离了出来。
之前不想分离出来时因为二维数据传递很麻烦,要不就是指针,要不就是自定义结构体,要不就是全局变量。
我选择用全局变量,后来索性就多用了几个全局变量,比如参数的标志位,最大和。
从代码中可以看到其实要改的只要3个部分:
(1)逻辑判定中判定出/h和/v,并且把文件名位置改成argv[i-1];
(2)在Find2DMax中写出/v情况的分支做法;
(3)在FindMax中写出/h情况的分支做法;
第一个很简单,不再赘述;第二个就是在枚举上下界的时候,让下界可以循环到上界的前一个就可以了。
第三个我暂时还没想出来,不过可以确定只需要在最底层的FindMax中改动;
测试结果:
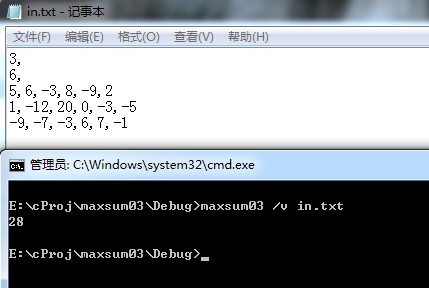
由于没有完全实现功能,所以我也不敢对复杂度下定论。
5.第五题与第四题基本上是没有区别的。
只需要改一下逻辑判断就可以了。因为在第四题的论述中,我们发现/h和/v是互不影响的,他们改动的就不是一个函数。
这次的作业令我获益匪浅:
(1)首先我学会了做软件或者程序的方法,那就是先做一个基本的功能,然后再慢慢地往上积累,循序渐进地开发,站在之前的基础上看世界,就能看得更高更远;
(2)切莫眼高手低,从12点做到现在已经5个多小时了,意思都模糊了。。以后有作业一定要早早开始做,不要想着临到时间了很快就会做完,看过之后才发现难度好大。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








