本节主要讨论K均值聚类和围绕中心点的划分PAM聚类。
K均值聚类:
最常见的划分方法是K均值聚类分析。从概念上讲, K均值算法如下:
(1) 选择K个中心点(随机选择K行);
(2) 把每个数据点分配到离它最近的中心点;
(3) 重新计算每类中的点到该类中心点距离的平均值(也就说,得到长度为p的均值向量,这里的p是变量的个数);
(4) 分配每个数据到它最近的中心点;
(5) 重复步骤(3)和步骤(4)直到所有的观测值不再被分配或是达到最大的迭代次数(R把10次作为默认迭代次数)。
K均值聚类能处理比层次聚类更大的数据集。另外,观测值不会永远被分到一类中。当我们提高整体解决方案时,聚类方案也会改动。但是均值的使用意味着所有的变量必须是连续的,并且这个方法很有可能被异常值影响。不像层次聚类方法, K均值聚类要求你事先确定要提取的聚类个数(这也是 K-means 算法的一个不足)(在每次调用函数时可能获得不同的方案)。同样, NbClust包可以用来作为参考。
例:葡萄酒数据的K均值聚类
data(wine, package="rattle")
head(wine)
df <- scale(wine[-1]) #变量值变化很大,所以在聚类前要将其标准化
wssplot(df)
library(NbClust)
set.seed(1234)
nc <- NbClust(df, min.nc=2, max.nc=15, method="kmeans")#决定聚类个数
par(opar)
table(nc$Best.n[1,])
0 1 2 3 10 12 14 15
2 1 4 15 1 1 1 1
barplot(table(nc$Best.n[1,]),
xlab="Numer of Clusters", ylab="Number of Criteria",
main="Number of Clusters Chosen by 26 Criteria")
set.seed(1234) #保证结果是可复制的
fit.km <- kmeans(df, 3, nstart=25)
fit.km$size
62 65 51
fit.km$centers #聚类中心
Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids
1 0.8328826 -0.3029551 0.3636801 -0.6084749 0.57596208 0.88274724 0.97506900
2 -0.9234669 -0.3929331 -0.4931257 0.1701220 -0.49032869 -0.07576891 0.02075402
3 0.1644436 0.8690954 0.1863726 0.5228924 -0.07526047 -0.97657548 -1.21182921
Nonflavanoids Proanthocyanins Color Hue Dilution Proline
1 -0.56050853 0.57865427 0.1705823 0.4726504 0.7770551 1.1220202
2 -0.03343924 0.05810161 -0.8993770 0.4605046 0.2700025 -0.7517257
3 0.72402116 -0.77751312 0.9388902 -1.1615122 -1.2887761 -0.4059428
aggregate(wine[-1], by=list(cluster=fit.km$cluster), mean)
#因为输出的聚类中心是基于标准化的数据,所以可以使用aggregate()函数和类的成员来得到原始矩阵中每一类的变量均值。
cluster Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids
1 1 13.67677 1.997903 2.466290 17.46290 107.96774 2.847581 3.0032258
2 2 12.25092 1.897385 2.231231 20.06308 92.73846 2.247692 2.0500000
3 3 13.13412 3.307255 2.417647 21.24118 98.66667 1.683922 0.8188235
Nonflavanoids Proanthocyanins Color Hue Dilution Proline
1 0.2920968 1.922097 5.453548 1.0654839 3.163387 1100.2258
2 0.3576923 1.624154 2.973077 1.0627077 2.803385 510.1692
3 0.4519608 1.145882 7.234706 0.6919608 1.696667 619.0588
# evaluate clustering
ct.km <- table(wine$Type, fit.km$cluster)
ct.km
1 2 3
1 59 0 0
2 3 65 3
3 0 0 48
library(flexclust)
randIndex(ct.km) #兰德指数:量化类型变量和类之间的协议。
ARI
0.897495
附:#data参数是用来分析的数值数据, nc是要考虑的最大聚类个数,而seed是一个随机数种子。
wssplot <- function(data, nc=15, seed=1234){
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:nc){
set.seed(seed)
wss[i] <- sum(kmeans(data, centers=i)$withinss)}
plot(1:nc, wss, type="b", xlab="Number of Clusters",
ylab="Within groups sum of squares")}
围绕中心点的划分PAM聚类
因为K均值聚类方法是基于均值的,所以它对异常值是敏感的。一个更稳健的方法是围绕中心点的划分(PAM)。与其用质心(变量均值向量)表示类,不如用一个最有代表性的观测值来表示(称为中心点)。 K均值聚类一般使用欧几里得距离,而PAM可以使用任意的距离来计算。因此, PAM可以容纳混合数据类型,并且不仅限于连续变量 。它算是k均值聚类算法的改进。
PAM算法如下:
(1) 随机选择K个观测值(每个都称为中心点);
(2) 计算观测值到各个中心的距离/相异性;
(3) 把每个观测值分配到最近的中心点;
(4) 计算每个中心点到每个观测值的距离的总和(总成本);
(5) 选择一个该类中不是中心的点,并和中心点互换;
(6) 重新把每个点分配到距它最近的中心点;
(7) 再次计算总成本;
(8) 如果总成本比步骤(4)计算的总成本少,把新的点作为中心点;
(9) 重复步骤(5)~(8)直到中心点不再改变。
你可以使用cluster包中的pam()函数使用基于中心点的划分方法。格式是pam(x, k,metric="euclidean", stand=FALSE),这里的x表示数据矩阵或数据框, k表示聚类的个数,metric表示使用的相似性/相异性的度量,而stand是一个逻辑值,表示是否有变量应该在计算
该指标之前被标准化。
例:对葡萄酒数据使用基于质心的划分方法
vlibrary(cluster)
set.seed(1234)
fit.pam <- pam(wine[-1], k=3, stand=TRUE)
fit.pam$medoids
Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids
[1,] 13.48 1.81 2.41 20.5 100 2.70 2.98 0.26
[2,] 12.25 1.73 2.12 19.0 80 1.65 2.03 0.37
[3,] 13.40 3.91 2.48 23.0 102 1.80 0.75 0.43
Proanthocyanins Color Hue Dilution Proline
[1,] 1.86 5.1 1.04 3.47 920
[2,] 1.63 3.4 1.00 3.17 510
[3,] 1.41 7.3 0.70 1.56 750
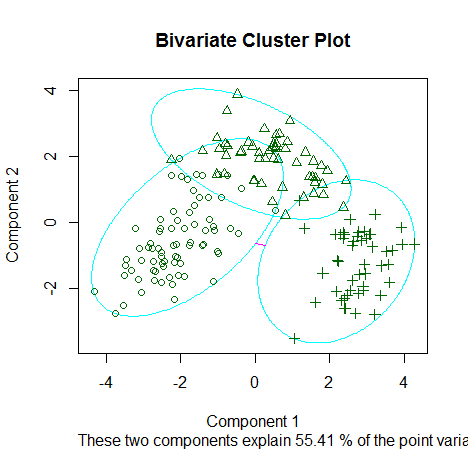
clusplot(fit.pam, main="Bivariate Cluster Plot")
# evaluate clustering
ct.pam <- table(wine$Type, fit.pam$clustering)
ct.pam
1 2 3
1 59 0 0
2 16 53 2
3 0 1 47
library(flexclust)
randIndex(ct.pam)#下降到0.7。貌似改进的PAM没有Kmean结果好
ARI
0.6994957





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








