POJ2826 An Easy Problem?!（线段交点，三角形面积）

最新推荐文章于 2022-06-26 20:46:58 发布

weixin_30493321

最新推荐文章于 2022-06-26 20:46:58 发布

阅读量70

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/hyp1231/p/7043495.html

本文介绍了一道经典的计算几何题目——如何计算二维平面上两条线段形成的凹槽能够收集多少雨水。通过向量和点运算的方法，文章详细解析了各种特殊情况的处理，并给出完整的C++实现代码。

题目链接：

　　http://poj.org/problem?id=2826

题目描述：

An Easy Problem?!

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width.

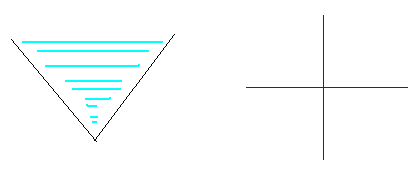
Your mission is to calculate how much rain these two boards can collect.

Input

The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x ₁, y ₁, x ₂, y ₂, x ₃, y ₃, x ₄, y ₄. ( x ₁, y ₁), ( x ₂, y ₂) are the endpoints of one board, and ( x ₃, y ₃), ( x ₄, y ₄) are the endpoints of the other one.

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.

Sample Input

Sample Output

1.00
0.00

题目大意：

　　给定二维平面上的两条固定的线段，求下雨的时候能装多少水

思路：

　　An easy problem……欺骗感情啊

　　好多需要注意的地方

　　因为情况很多但很类似

　　我们可以把两个线段用点加向量的方式表示，并且保证v1比v2的极角小（均在[0,π)之间）

　　那么现在有哪些情况一定输出0呢

　　1、任一条线段水平

　　2、线段无交点

　　3、向量重合

　　4、某一个线段把另一个线段遮住了（如图）

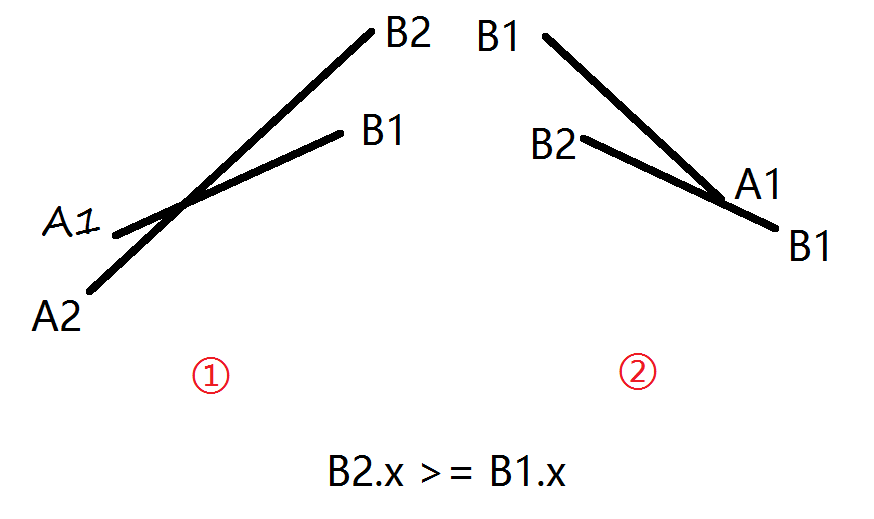
　　5、B1 B2 重合

　　然后我们依次求出线段交点（C1），以及过B1 B2中y较小的点（tmp）水平的直线与另一条线段的交点（C2）

　　叉乘解三角形面积即可

代码：

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <algorithm>
 4 #include <cstring>
 5 #include <cmath>
 6 using namespace std;
 7 
 8 const double EPS = 1e-10;    //精度系数
 9 
10 struct Point {
11     double x, y;
12     Point(double x = 0, double y = 0) :x(x), y(y) {}
13 };    //点的定义
14 
15 typedef Point Vector;    //向量的定义
16 
17 int dcmp(double x) {
18     if (fabs(x) < EPS)return 0; else return x < 0 ? -1 : 1;
19 }    //与0的关系
20 
21 Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }    //向量加法
22 Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }    //向量减法
23 Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }        //向量数乘
24 bool operator == (const Point& a, const Point& b) {
25     return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
26 }    //点相等
27 
28 double Angle(Vector A) { return atan2(A.y, A.x); }    //向量极角
29 
30 double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }    //向量叉乘
31 
32 bool SegmentProperIntersection(Point& a1, Point& a2, Point& b1, Point& b2) {
33     double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1),
34         c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
35     return dcmp(c1)*dcmp(c2) <= 0 && dcmp(c3)*dcmp(c4) <= 0;
36 }    //判断两线段相交（含端点）
37 
38 Point LineIntersectionPoint(Point A1, Point B1, Point A2, Point B2) {
39     double t1 = ((A1.y - A2.y)*(B2.x - A2.x) - (A1.x - A2.x)*(B2.y - A2.y)) /
40         ((B1.x - A1.x)*(B2.y - A2.y) - (B1.y - A1.y)*(B2.x - A2.x));
41     return A1 + (B1 - A1)*t1;
42 }    //返回直线交点
43 
44 double Area2(Point& A, Point& B, Point& C) { return Cross(B - A, C - A); }
45 //AB,AC向量围成的三角形面积的两倍
46 
47 Point A1, B1, A2, B2;
48 
49 int main() {
50     int t;
51     cin >> t;
52     while (t--) {
53         scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &A1.x, &A1.y, &B1.x, &B1.y, &A2.x, &A2.y, &B2.x, &B2.y);
54         Vector v1 = B1 - A1, v2 = B2 - A2, u(1, 0);
55         if (dcmp(Cross(v1, u)) == 0 || dcmp(Cross(v1, u)) == 0) { printf("0.00\n"); continue; }    //情况1
56         if (!SegmentProperIntersection(A1, B1, A2, B2)) { printf("0.00\n"); continue; }    //情况2
57         double d1 = Angle(v1), d2 = Angle(v2);
58         if (dcmp(d1) < 0) { swap(A1, B1); v1 = v1*-1; d1 = Angle(v1); }
59         if (dcmp(d2) < 0) { swap(A2, B2); v2 = v2*-1; d2 = Angle(v2); }
60         if (dcmp(d1 - d2) == 0) { printf("0.00\n"); continue; }    //情况3
61         if (d1 > d2) { swap(d1, d2); swap(v1, v2); swap(A1, A2); swap(B1, B2); }
62         if (B2.x >= B1.x || B1 == B2) { printf("0.00\n"); continue; }    //情况4 5
63         Point C1 = LineIntersectionPoint(A1, B1, A2, B2), tmp, N1, N2;    //线段交点
64         if (B1.y < B2.y)tmp = B1, N1 = A2, N2 = B2;
65         else tmp = B2, N1 = A1, N2 = B1;    //求出B1 B2 中y值较小的点
66         Point C2 = LineIntersectionPoint(tmp, tmp + u, N1, N2);    //三角形第三个点
67         double ans = fabs(Area2(C1, C2, tmp)) / 2;
68         printf("%.2lf\n", ans);
69     }
70 }

转载于:https://www.cnblogs.com/hyp1231/p/7043495.html