215 Kth Largest Element in an Array 快排

 

题目：在无序的数组中找到第k大的元素，也就是若长度为n的数组从小到大排列时，下标为n-k的元素。

注意Example2：第4大的元素是4，也就是数组中出现的两个5分别是第2大和第3大的数字。                   

解法一：直接利用sort函数排序后，取第k大的元素。

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        return nums[nums.size() - k];
    }
};

 

解法二：快排

时间复杂度是：O(n)

 

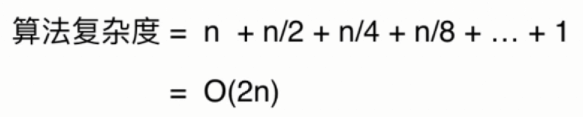
注意几个问题：

1）k的取值：是不变的啊！ 不会因为递归时在privot的左边或者右边寻找而改变，因为nums的长度n是不变的，元素的下标也是不变的；

2）partition函数递归调用自己时是要加return的！不然会报错。

class Solution {
public:
    
     int partition(vector<int>& nums, int k, int l, int r){
       int n = nums.size();
        swap(nums[l],nums[rand()%(r-l+1)+l]);   //生成随机数
        int p = nums[l];
        
        //nums[l+1...i) <=v ; nums(j...r] >=v i和j 是需要考察的元素，所以是开区间
        int i = l+1, j = r;     //初始定义区间为空
        while(true){
            while(i<=r && nums[i]<p)
                i++;
            while(j>=l+1 && nums[j]>p)
                j--;
            if(i>j) break;
            swap(nums[i], nums[j]);
            i++;
            j--;
        }
        swap(nums[l], nums[j]);
        
        if(j == n-k) return nums[j];
        else if(j < n-k) return partition(nums, k, j+1,r);
        else return partition(nums, k, l, j-1);
        
    }
    
    int findKthLargest(vector<int>& nums, int k) {
        srand(time(NULL));
        int n = nums.size();
        return partition(nums, k, 0, n-1);
        
    }

};

 终于把快排思想的写对了，前一天晚上一直在报错，因为上面提到的两个点没有想明白，还是早上效率高 :)

解法二：思路是将比privot大的元素放到privot左边， 小的放到privot右边。

class Solution {
public:
    
     int partition(vector<int>& nums, int k, int l, int r){
       int n = nums.size();
        swap(nums[l],nums[rand()%(r-l+1)+l]);   //生成随机数
        int p = nums[l];
        
        //nums[l+1...i) <=v ; nums(j...r] >=v i和j 是需要考察的元素，所以是开区间
        int i = l+1, j = r;     //初始定义区间为空
        while(true){
            while(i<=r && nums[i]>p)
                i++;
            while(j>=l+1 && nums[j]<p)
                j--;
            if(i>j) break;
            swap(nums[i], nums[j]);
            i++;
            j--;
        }
        swap(nums[l], nums[j]);
        
        if(j == k-1) return nums[j];
        else if(j < k-1) return partition(nums, k, j+1, r);
        else return partition(nums, k, l, j-1);
        
    }
    
    int findKthLargest(vector<int>& nums, int k) {
        srand(time(NULL));
        int n = nums.size();
        return partition(nums, k, 0, n-1);
        
    }

};

 

转载于:https://www.cnblogs.com/Bella2017/p/10128957.html